UMAP 在稀疏数据上
有时数据集会变得非常庞大,且维度可能非常非常高。然而,在许多此类情况下,数据本身是稀疏的——也就是说,虽然有很多很多特征,但任何给定的样本只观察到少量非零特征。在这种情况下,使用稀疏矩阵数据结构可以更有效地表示数据,从而节省内存。很难找到能直接处理此类稀疏数据的降维技术——通常会应用像 sklearn 中的 TruncatedSVD 这样接受稀疏矩阵输入的线性基本技术,以便将数据转换为适合其他更高级降维技术的格式。对于 UMAP 来说,这并非必要——UMAP 可以直接在稀疏矩阵输入上运行。本教程将通过几个示例来演示如何做到这一点。首先我们需要加载一些库。显然我们需要 numpy,但我们也会使用 scipy.sparse,它提供了稀疏矩阵数据结构。我们的一个示例将纯粹是数学性的,为此我们将使用 sympy;另一个示例基于文本,我们将使用 sklearn(特别是 sklearn.feature_extraction.text)。除此之外,我们还需要 umap 和绘图工具。
import numpy as np
import scipy.sparse
import sympy
import sklearn.datasets
import sklearn.feature_extraction.text
import umap
import umap.plot
import matplotlib.pyplot as plt
%matplotlib inline
一个数学示例
我们的第一个示例纯粹从数学角度构建了一个稀疏数据矩阵。此示例受到 John Williamson 工作的启发,如果您还没有看过那项工作,强烈建议您去看一下。我们将要考虑的数据集是整数。我们将每个整数表示为一个向量,该向量反映了它对不同素数的整除性。因此,我们的特征空间是素数空间(小于或等于我们考虑的最大整数)——这可能是非常高维的。实际上,任何给定整数只能被少量不同的素数整除,所以每个样本将主要由零组成(所有不能整除该数的素数),因此我们将得到一个非常稀疏的数据集。
要开始,我们需要所有素数的列表。幸运的是,我们有 sympy 库可以使用,只需调用 primerange 就可以快速获取这些信息。我们还需要一个字典,将不同的素数映射到它们在数据结构中对应的列号;实际上,我们只是在枚举素数。
primes = list(sympy.primerange(2, 110000))
prime_to_column = {p:i for i, p in enumerate(primes)}
现在我们需要将数据构建成一种易于放入稀疏矩阵的格式。此时,了解一些稀疏矩阵数据结构的背景知识很有用。为此,我们将使用所谓的 “LIL”格式。LIL 是“List of Lists”(列表的列表)的缩写,因为数据在内部就是这样存储的。有一个包含所有行的列表,每行存储为一个列表,给出非零项的列索引。为了存储数据值,有一个并行的结构,其中包含给定行和列对应项的值。
要将数据整理成这种格式,我们需要构建这样的列表的列表。我们可以通过迭代所有整数(直到一个固定界限),并为每个整数(即我们数据集中的每一行)生成将是非零的列索引列表来实现。列索引将简单地是对应于整除该数的素数的索引。由于 sympy 有一个函数 primefactors 可以返回任何整数的唯一素因数列表,我们只需通过我们的字典进行映射,将素数转换为列号即可。
与此同时,我们将构建相应的值结构,以便插入到矩阵中。由于我们只关注整除性,所以每个非零项的值都将是 1,因此我们只需为每一行添加一个长度合适的 1 列表即可。
%%time
lil_matrix_rows = []
lil_matrix_data = []
for n in range(100000):
prime_factors = sympy.primefactors(n)
lil_matrix_rows.append([prime_to_column[p] for p in prime_factors])
lil_matrix_data.append([1] * len(prime_factors))
CPU times: user 2.07 s, sys: 26.4 ms, total: 2.1 s
Wall time: 2.1 s
现在我们需要将其放入稀疏矩阵中。幸运的是,scipy.sparse 包使得这很容易,而且我们已经以相当有用的结构构建了数据。首先,我们创建一个正确格式(LIL)和正确形状(行数与我们生成的行数相同,列数与素数数量相同)的稀疏矩阵。然而,这基本上只是一个空矩阵。我们可以通过将 rows 属性设置为我们生成的行,并将 data 属性设置为相应的值结构(全为 1)来解决这个问题。结果是一个稀疏矩阵数据结构,可以很容易地操作并轻松转换为其他稀疏矩阵格式。
factor_matrix = scipy.sparse.lil_matrix((len(lil_matrix_rows), len(primes)), dtype=np.float32)
factor_matrix.rows = np.array(lil_matrix_rows)
factor_matrix.data = np.array(lil_matrix_data)
factor_matrix
<100000x10453 sparse matrix of type '<class 'numpy.float32'>'
with 266398 stored elements in LInked List format>
如您所见,我们有一个包含 100000 行和超过 10000 列的矩阵。如果将其存储为 numpy 数组,将占用大量内存。然而,实际上只有大约 260000 个非零项,而这正是我们真正需要存储的全部内容,这使得它更加紧凑。
现在的问题是如何将这种稀疏矩阵结构输入到 UMAP 中,以便让它学习一个嵌入。答案出奇地简单——我们只需将其直接传递给 fit 方法。就像其他可以处理稀疏输入的 sklearn 估计器一样,UMAP 会检测到稀疏矩阵并执行正确的操作。
%%time
mapper = umap.UMAP(metric='cosine', random_state=42, low_memory=True).fit(factor_matrix)
CPU times: user 9min 36s, sys: 6.76 s, total: 9min 43s
Wall time: 9min 7s
这很容易!但这真的有效吗?我们可以轻松绘制结果
umap.plot.points(mapper, values=np.arange(100000), theme='viridis')
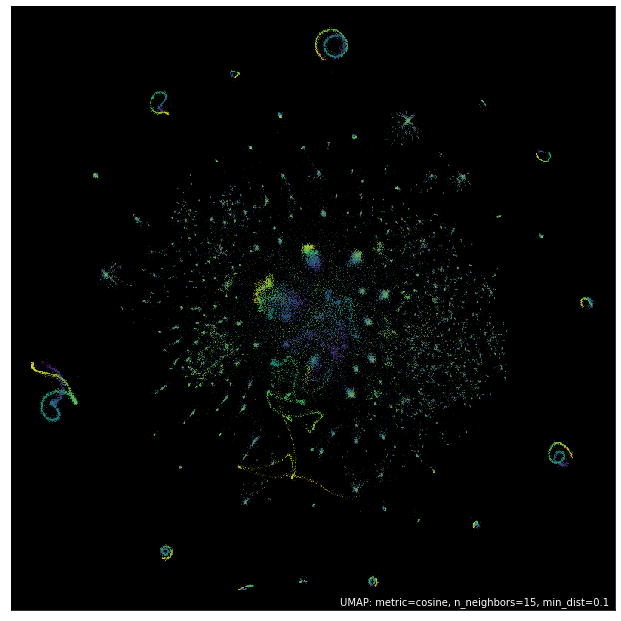
这与 John Williamson 得到的结果 非常吻合,前提是我们只使用了 100,000 个整数而不是 1,000,000 个,以确保大多数用户能够运行此示例(完整的 100 万个可能需要较大的内存计算节点)。所以看起来这工作得很好。下一个问题是我们能否使用 transform 功能将新数据映射到这个空间。为了测试这一点,我们需要更多数据。幸运的是,还有更多整数。我们将获取接下来的 10,000 个,并将它们放入稀疏矩阵中,就像我们处理前 100,000 个一样。
%%time
lil_matrix_rows = []
lil_matrix_data = []
for n in range(100000, 110000):
prime_factors = sympy.primefactors(n)
lil_matrix_rows.append([prime_to_column[p] for p in prime_factors])
lil_matrix_data.append([1] * len(prime_factors))
CPU times: user 214 ms, sys: 1.99 ms, total: 216 ms
Wall time: 222 ms
new_data = scipy.sparse.lil_matrix((len(lil_matrix_rows), len(primes)), dtype=np.float32)
new_data.rows = np.array(lil_matrix_rows)
new_data.data = np.array(lil_matrix_data)
new_data
<10000x10453 sparse matrix of type '<class 'numpy.float32'>'
with 27592 stored elements in LInked List format>
要映射我们生成的新数据,我们只需将其传递给我们训练好的模型的 transform 方法。这有点慢,但确实有效。
new_data_embedding = mapper.transform(new_data)
然后我们可以绘制结果。由于这次我们只获得了点的位置(而不是模型),我们将不得不依靠 matplotlib 来进行绘图。
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
plt.scatter(new_data_embedding[:, 0], new_data_embedding[:, 1], s=0.1, c=np.arange(10000), cmap='viridis')
ax.set(xticks=[], yticks=[], facecolor='black');
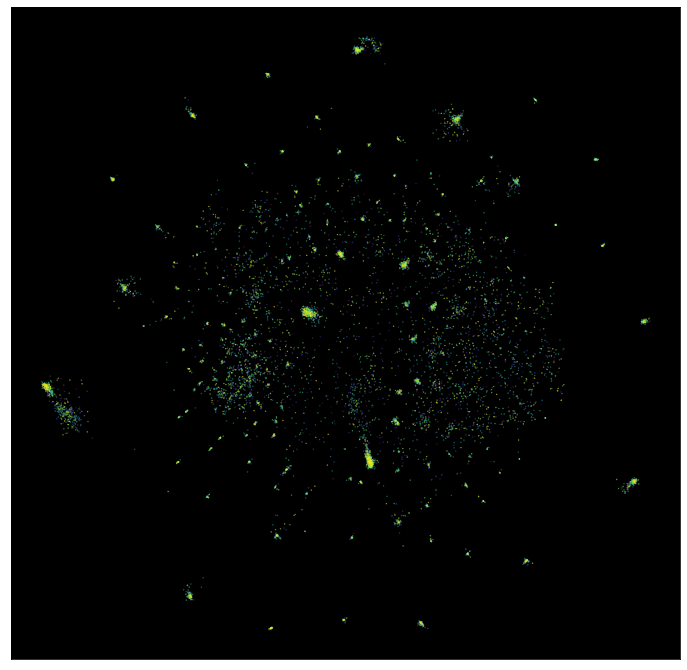
在这种情况下,颜色比例尺是不同的,但您可以看到数据已被映射到与原始嵌入中看到的各种结构相对应的位置。因此,即使是大型稀疏数据,我们也可以对数据进行嵌入,甚至可以向嵌入中添加新数据。
一个文本分析示例
让我们看一个更经典的机器学习示例,处理稀疏高维数据——即处理文本文档。文本上的机器学习很困难,并且有大量的相关文献,但目前我们只考虑一种基本方法。文本机器学习的困难之一是将语言转换为数字,因为归根结底,数字才是大多数机器学习算法所理解的(至少核心是这样)。对于文档来说,最直接的方法之一就是所谓的 “词袋”(bag-of-words)模型。在这个模型中,我们将文档视为其中所包含词语的简单多重集合——我们完全忽略词语顺序。结果可以视为一个数据矩阵,其中特征空间是出现在任何文档中的所有词语的集合,文档表示为一个向量,其中第 i 个条目的值是第 i 个词语在该文档中出现的次数。这是一种非常常见的方法,例如,如果您将 sklearn 的 CountVectorizer 应用于文本数据集,就会得到这种结果。这种方法的缺点是特征空间通常 非常 大,因为整个文档语料库中出现的每一个词语都有一个特征。然而,数据是稀疏的,因为大多数文档只使用了总词汇量的一小部分。因此,CountVectorizer(以及 sklearn 中其他类似的特征提取工具)的默认输出格式是 scipy.sparse 格式的矩阵。
对于这个示例,我们将使用经典的 20newsgroups 数据集,它是来自旧 NNTP 新闻组系统的消息样本,涵盖 20 个不同的新闻组。sklearn.datasets 模块可以轻松获取数据,事实上,我们可以获取预向量化版本,省去自己运行 CountVectorizer 的麻烦。我们将获取训练集和测试集以供以后使用。
news_train = sklearn.datasets.fetch_20newsgroups_vectorized(subset='train')
news_test = sklearn.datasets.fetch_20newsgroups_vectorized(subset='test')
如果我们查看实际获取到的数据,我们会看到 sklearn 已经运行了 CountVectorizer 并以稀疏矩阵格式生成了数据。
news_train.data
<11314x130107 sparse matrix of type '<class 'numpy.float64'>'
with 1787565 stored elements in Compressed Sparse Row format>
在这种情况下,稀疏矩阵格式的价值立竿见影;尽管只有 11,000 个样本,但却有 130,000 个特征!如果数据存储在标准的 numpy 数组中,我们将占用 10GB 的内存!而且大部分内存都只是在一遍又一遍地存储数字零。而稀疏矩阵格式的数据在大多数机器上很容易适合内存。这种数据维度对于文本工作负载来说非常常见。
然而,原始计数并不理想,因为像“the”和“and”这样的常用词会在大多数文档中占据主导地位,而对文档的实际内容贡献的信息却很少。我们可以通过使用 sklearn 中的 TfidfTransformer 来纠正这个问题,它会将数据转换为 TF-IDF 格式。有很多方法可以思考 TF-IDF 所做的转换,但我喜欢直观地将其理解如下:一个词的信息内容可以认为是(大约)与该词频率的负对数成正比;一个词使用得越频繁,它携带的信息往往越少,而不常用词携带更多信息。TF-IDF 所做的事情可以被认为是根据与列相关的词语信息内容对列进行重新加权。因此,像“the”和“and”这样的常用词会被降权,因为它们对文档的信息贡献较少,而不常用词则被认为更重要,其相关列会得到升权。我们可以将这种转换应用于训练集和测试集(使用在训练集上训练的同一个转换器)。
tfidf = sklearn.feature_extraction.text.TfidfTransformer(norm='l1').fit(news_train.data)
train_data = tfidf.transform(news_train.data)
test_data = tfidf.transform(news_test.data)
结果仍然是一个稀疏矩阵,因为 TF-IDF 完全不改变零元素,也不改变特征的数量。
train_data
<11314x130107 sparse matrix of type '<class 'numpy.float64'>'
with 1787565 stored elements in Compressed Sparse Row format>
现在我们需要将这种非常高维的数据传递给 UMAP。与其他一些非线性降维技术不同,我们不需要先应用 PCA 将数据降到合理的维度;也不需要使用其他技术将数据缩减为能够表示为密集 numpy 数组的形式;我们可以直接处理 130,000 维的稀疏矩阵。
%%time
mapper = umap.UMAP(metric='hellinger', random_state=42).fit(train_data)
CPU times: user 8min 40s, sys: 3.07 s, total: 8min 44s
Wall time: 8min 43s
现在我们可以绘制结果,并根据数据的目标变量(即帖子来自哪个新闻组)进行标注。
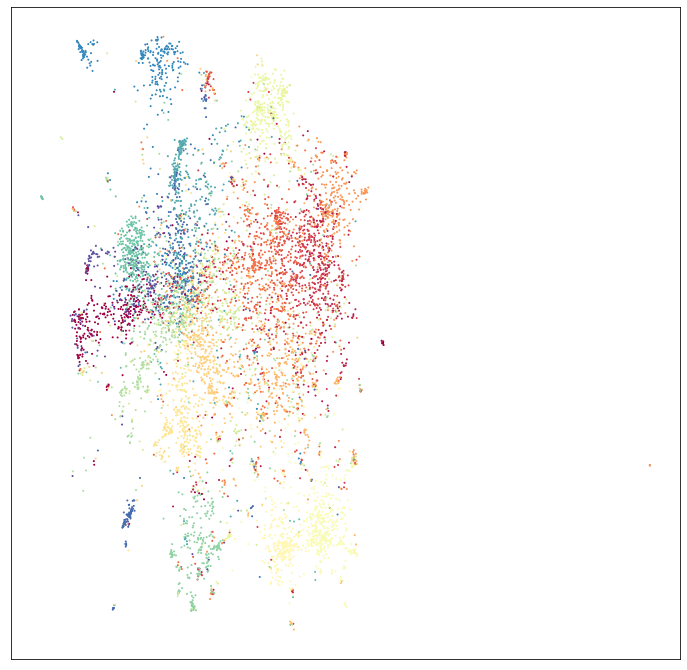
umap.plot.points(mapper, labels=news_train.target)
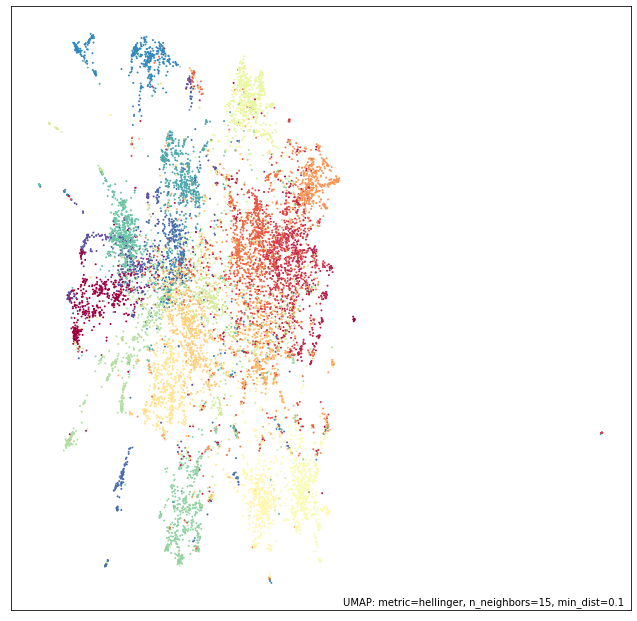
我们可以看到,即使直接从 130,000 维空间降到仅 2 维,UMAP 在分离许多不同新闻组方面也做得相当不错。
现在我们可以尝试使用 transform 方法将测试数据添加到同一空间中。
test_embedding = mapper.transform(test_data)
虽然这在计算上有些耗费资源,但确实有效,我们可以绘制最终结果
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
plt.scatter(test_embedding[:, 0], test_embedding[:, 1], s=1, c=news_test.target, cmap='Spectral')
ax.set(xticks=[], yticks=[]);