降维实现的性能比较

不同的降维技术可能具有截然不同的计算复杂度。除了算法本身，实现方式也会产生影响。这两个因素对实际运行给定降维算法所需的时间有着重要作用。此外，您尝试处理的数据性质也会产生影响——这主要涉及原始数据的维度。在这里，我们将简要介绍一些降维实现的性能特征。

首先，让我们加载所需的基本工具——显然包括 numpy 和 pandas，但也需要用于获取和重采样数据的工具，以及 time 模块以便进行一些基础的性能测试。

import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.utils import resample
import time

接下来，我们需要实际的降维实现。为了便于解释，我们主要使用 scikit-learn，但为了比较，我们还将包括 MulticoreTSNE 对 t-SNE 的实现，其性能明显优于当前的 scikit-learn t-SNE。

from sklearn.manifold import TSNE, LocallyLinearEmbedding, Isomap, MDS, SpectralEmbedding
from sklearn.decomposition import PCA
from MulticoreTSNE import MulticoreTSNE
from umap import UMAP

接下来，我们需要绘图工具，当然还有一些数据来处理。对于这次性能比较，我们将默认使用流形学习的现行标准基准测试：MNIST 数字数据集。我们可以使用 scikit-learn 的 fetch_mldata 来为我们获取数据。

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

sns.set(context='notebook',
        rc={'figure.figsize':(12,10)},
        palette=sns.color_palette('tab10', 10))

mnist = fetch_openml('Fashion-MNIST', version=1)

现在是时候开始考察性能了。首先，让我们看看性能如何随数据集大小的增加而变化。

性能随数据集大小的变化

随着数据集大小的增加，给定降维算法的运行时间会以不同的速率增加。如果您想在更大的数据集上运行您的算法，您不仅会关心在单个小型数据集上的比较运行时间，还会关心随着数据集变大，性能如何扩展。我们可以通过从 MNIST 数字中进行子采样（通过 scikit-learn 便捷的 resample 工具）并查看不同大小子样本的运行时间来模拟这种情况。由于此处涉及一些随机性（子样本选择和某些具有随机方面的算法），我们将希望对每种数据集大小运行几个示例。我们可以轻松地将所有这些打包在一个简单的函数中，该函数给定一个算法，将返回一个包含数据集大小和运行时间的便捷 pandas 数据框。

def data_size_scaling(algorithm, data, sizes=[100, 200, 400, 800, 1600], n_runs=5):
    result = []
    for size in sizes:
        for run in range(n_runs):
            subsample = resample(data, n_samples=size)
            start_time = time.time()
            algorithm.fit(subsample)
            elapsed_time = time.time() - start_time
            del subsample
            result.append((size, elapsed_time))
    return pd.DataFrame(result, columns=('dataset size', 'runtime (s)'))

现在我们只需对各种降维实现都运行这个函数，以便查看结果。由于我们不知道这些运行可能需要多长时间，我们将从一个非常小的样本集开始，只扩展到 1600 个样本。

all_algorithms = [
    PCA(),
    UMAP(),
    MulticoreTSNE(),
    LocallyLinearEmbedding(),
    SpectralEmbedding(),
    Isomap(),
    TSNE(),
    MDS(),
]
performance_data = {}
for algorithm in all_algorithms:
    alg_name = str(algorithm)
    if 'MulticoreTSNE' in alg_name:
        alg_name = 'MulticoreTSNE'
    else:
        alg_name = alg_name.split('(')[0]

    performance_data[alg_name] = data_size_scaling(algorithm, mnist.data, n_runs=3)

现在让我们绘制结果，以便了解情况。我们将使用 seaborn 的回归图来插值有效的缩放比例。

for alg_name, perf_data in performance_data.items():
    sns.regplot('dataset size', 'runtime (s)', perf_data, order=2, label=alg_name)
plt.legend();

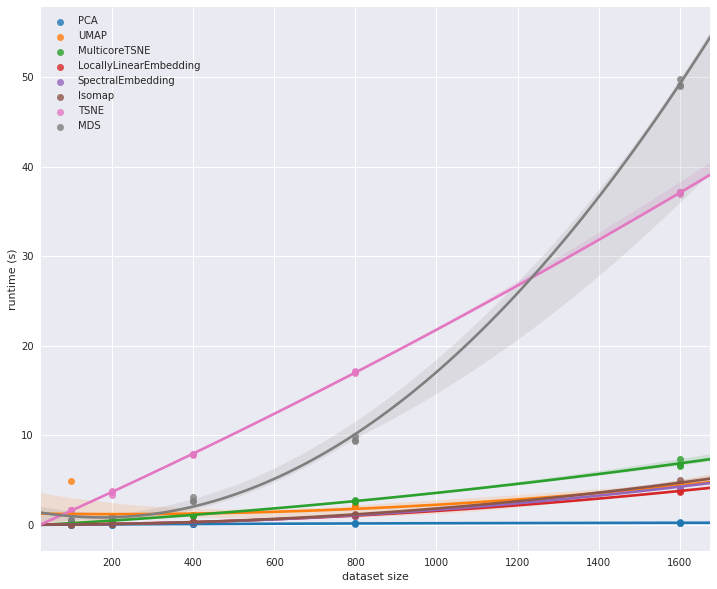
我们可以立即看到这里有一些异常值。scikit-learn 的 t-SNE 明显比大多数其他算法慢得多。然而，它不像 MDS 那样具有可伸缩性；对于更大的数据集，MDS 将很快变得完全无法处理。同时，MulticoreTSNE 表明 t-SNE 可以相当有效地运行。除了 PCA 是迄今为止最快的选项之外，很难判断其他实现的情况。要了解更多，我们需要查看在更大数据集上的运行时间。MDS 和 scikit-learn 的 t-SNE 都需要太长时间运行，所以让我们将范围限制在性能最快的实现，看看当我们扩展到更大数据集时会发生什么。

fast_algorithms = [
    PCA(),
    UMAP(),
    MulticoreTSNE(),
    LocallyLinearEmbedding(),
    SpectralEmbedding(),
    Isomap(),
]
fast_performance_data = {}
for algorithm in fast_algorithms:
    alg_name = str(algorithm)
    if 'MulticoreTSNE' in alg_name:
        alg_name = 'MulticoreTSNE'
    else:
        alg_name = alg_name.split('(')[0]

    fast_performance_data[alg_name] = data_size_scaling(algorithm, mnist.data,
                                                   sizes=[800, 1600, 3200, 6400, 12800], n_runs=3)

for alg_name, perf_data in fast_performance_data.items():
    sns.regplot('dataset size', 'runtime (s)', perf_data, order=2, label=alg_name)
plt.legend();

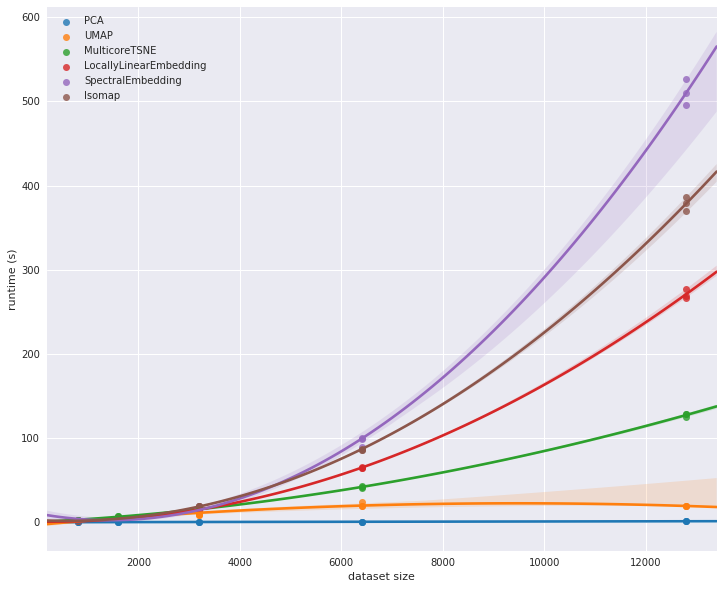
在这一点上，我们开始看到不同实现之间的一些显著差异。在之前的图中，MulticoreTSNE 看起来比其他一些算法要慢，但当我们扩展到更大的数据集时，我们看到它的相对缩放性能远优于 scikit-learn 中 Isomap、谱嵌入和局部线性嵌入的实现。

也许值得进一步扩展——直到完整的 MNIST 数字数据集。为了在合理的时间内完成，我们将不得不将注意力限制在更小的实现子集上。我们将精简到只剩下 MulticoreTSNE、PCA 和 UMAP。

very_fast_algorithms = [
    PCA(),
    UMAP(),
    MulticoreTSNE(),
]
vfast_performance_data = {}
for algorithm in very_fast_algorithms:
    alg_name = str(algorithm)
    if 'MulticoreTSNE' in alg_name:
        alg_name = 'MulticoreTSNE'
    else:
        alg_name = alg_name.split('(')[0]

    vfast_performance_data[alg_name] = data_size_scaling(algorithm, mnist.data,
                                                    sizes=[3200, 6400, 12800, 25600, 51200, 70000], n_runs=2)

for alg_name, perf_data in vfast_performance_data.items():
    sns.regplot('dataset size', 'runtime (s)', perf_data, order=2, label=alg_name)
plt.legend();

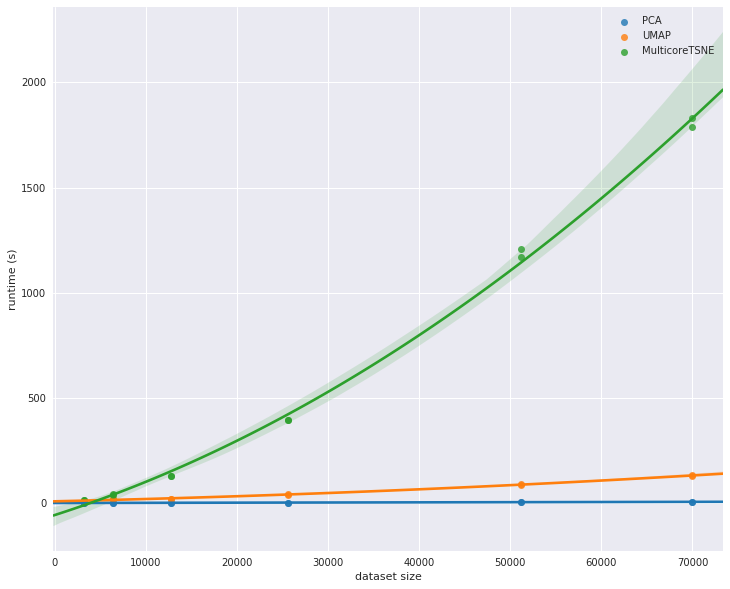
在这里，我们看到 UMAP 相对于 t-SNE 的优势真正凸显出来。虽然 UMAP 明显比 PCA 慢，但其缩放性能显著优于 MulticoreTSNE，对于更大的数据集，这种差异只会继续扩大。

关于性能随数据集大小变化的探讨到此结束。简短总结是：PCA 是迄今为止最快的选择，但为了这种速度，您可能会牺牲很多。UMAP 虽然在速度上无法与 PCA 竞争，但在此处探讨的实现中，它在性能方面显然是次优的选择。考虑到 UMAP 能够提供的结果质量，我们认为它显然是降维的一个好选择。