使用互信息 k-NN 图改进相似类别的分离

本文简要解释了原始图表示的连通性如何不利地影响最终的 UMAP 嵌入。

在默认 UMAP 中，构建一个加权 k 最近邻 (k-NN) 图（该图根据某个距离度量将每个数据点连接到其 𝑘 个最近邻），并用于生成数据集的初始拓扑表示。

然而，先前的研究表明，使用加权 k-NN 图可能无法准确表示高维数据集的基础局部结构。k-NN 图相对容易受到“维度诅咒”和相关的距离集中效应（即在高维空间中距离相似）的影响，以及枢纽效应（即某些点在高度连接时变得极具影响力）。这会扭曲高维数据的局部表示，从而降低其在各种基于相似度的机器学习任务中的性能。

最近一篇题为 Clustering with UMAP: Why and How Connectivity Matters 的论文提出了一种改进 UMAP 算法图构建阶段的方法，该方法使用加权互信息 k-NN 图而不是其香草版本，以减少不希望的距离集中和枢纽效应。

如这篇论文中所讨论的，互信息 k-NN 图已被证明在应对“维度诅咒”时具有许多理想的特性。然而，使用互信息 k-NN 图而非原始 k-NN 图的一个缺陷是它通常包含断开的组件和潜在的孤立顶点。

这违反了 UMAP 的主要假设之一：“流形是局部连通的。”为了解决孤立组件的问题，作者考虑了以前用于增强互信息 k-NN 图连通性的不同方法。

  1. NN：为了最小化连接孤立顶点并满足基础流形是局部连通的假设，我们在每个孤立顶点与其原始最近邻之间添加一条无向边（de Sousa, Rezende, and Batista 2013）。请注意，生成的图可能仍然包含断开的组件。

  2. MST-min：为了获得连通图，向已使用基于相似度度量加权的互信息 k-NN 图中添加最大生成树的最小数量的边（Ozaki et al. 2011）。我们通过计算距离的最小生成树来调整此方法。

  3. MST-all：添加 MST 的所有边。

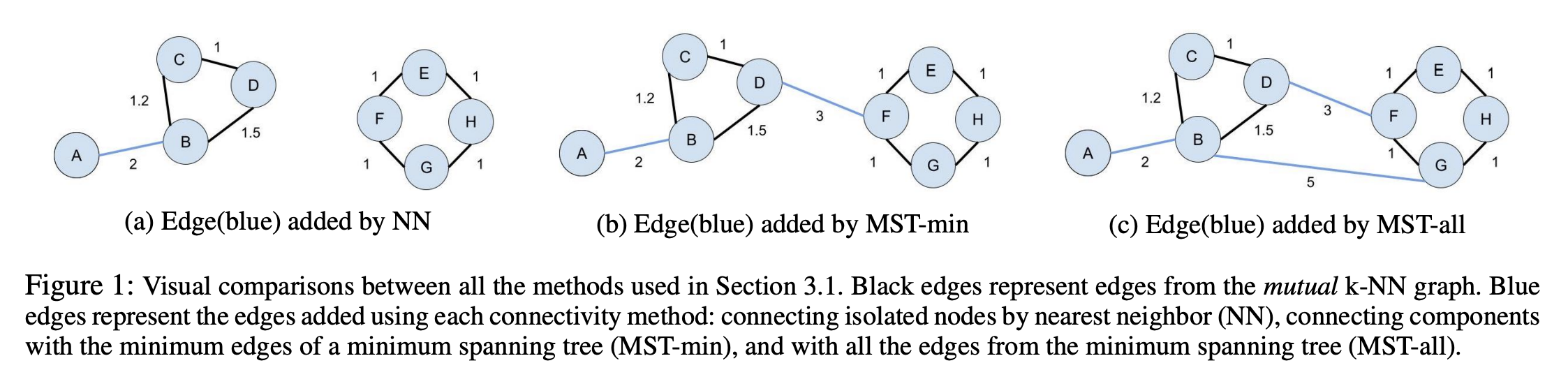
_images/mutual_nn_umap_connectivity.png

他们还有不同的方法来获取每个点 x_i 的新局部邻域。

  1. Adjacent Neighbors（相邻邻居）：仅考虑在连通互信息 k-NN 图中与 x_i 直接连接（相邻）的邻居。

  2. Path Neighbors（路径邻居）：使用最短路径距离来查找相对于连通互信息 k-NN 图与 x_i 最近的 k 个新点。此最短路径距离可被视为一种新的距离度量，因为它直接符合 UMAP 对扩展伪度量空间的定义。

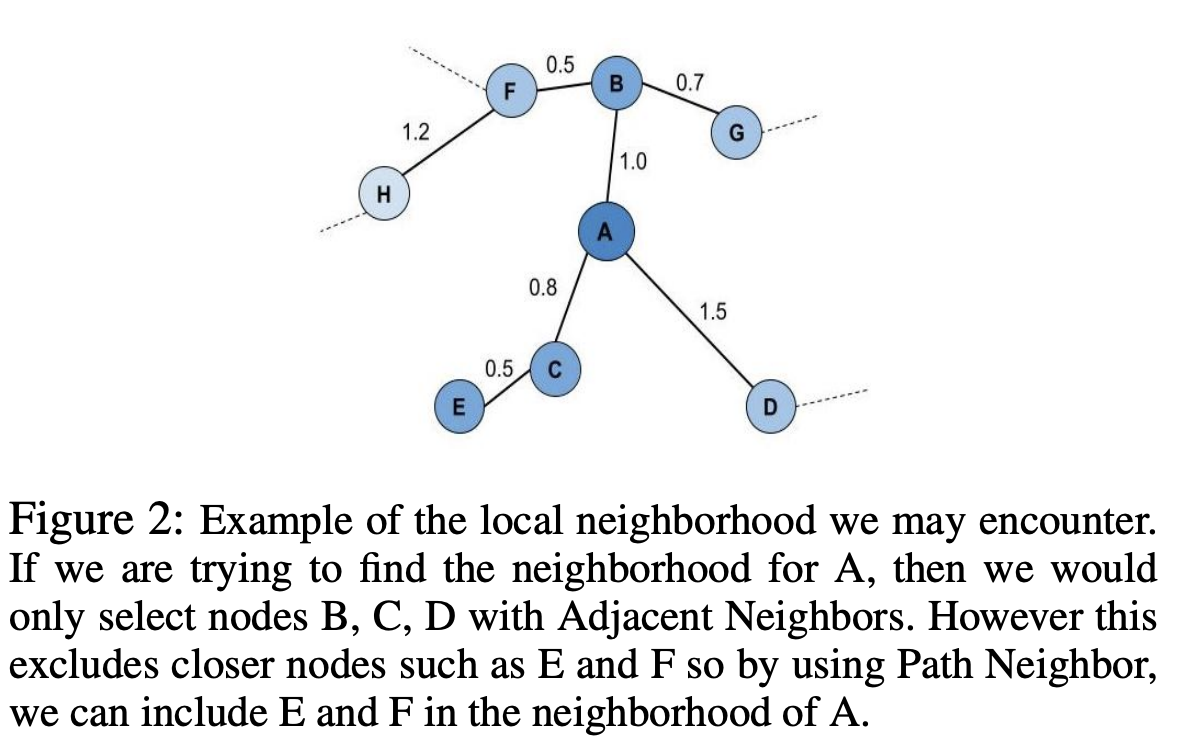
_images/mutual_nn_umap_lc.png

结果可视化

为了了解使用互信息 k-NN 图与原始 k-NN 图作为 UMAP 的起始拓扑之间的差异，我们使用每种讨论的方法可视化了为 MNIST、FMNIST 和 20 NG Count Vectors 生成的 2D 投影。所有用于重现结果和可视化的代码片段，请参考此 Github 仓库。我们将很快将其作为一种模式添加到原始实现中。

我们将从 MNIST 数字开始，这是一个包含 70,000 张手写数字灰度图像的集合。

_images/mutual_nn_umap_MNIST.png

总的来说，对于大多数基于互信息 k-NN 图的向量，无论连通性如何（NN、MST 变体），相似类别之间的分离都比原始 UMAP 向量更好。将互信息 k-NN 图中的孤立顶点连接到其原始最近邻，可以在相似类别之间产生期望的分离，例如 MNIST 中的 4、7、9。这符合我们的直觉，因为互信息 k-NN 图先前已被证明是一种有用的方法，可以移除仅微弱相似的点之间的边。

Fashion-MNIST(FMNIST) 数据集也观察到类似的结果，这是一个包含 70,000 张时尚物品灰度图像的集合。

_images/mutual_nn_umap_FMNIST.png

对于 FMNIST 数据集，使用上述方法生成的向量保留了服装类别（T 恤/上衣、外套、裤子等）与鞋类类别（凉鞋、运动鞋、踝靴）之间的全局结构，同时也清晰地描绘了鞋类类别之间的分离。这与原始 UMAP 形成对比，原始 UMAP 在相似类别（如鞋类类别）之间的分离较差。

对于 MNIST 和 FMNIST，简单地将孤立顶点连接到其最近邻的 NN 方法导致向量空间中散布着多个小点簇。考虑到使用 NN 进行连通性处理仍然可能导致最终的流形被分解成许多小组件，这一点是合理的。

公平地假设用“更高连通性”增强互信息 k-NN 图总是更好的，因为它减少了点的随机散布。然而，过高的连通性，例如 MST-all，也可能带来负面影响，这在论文中进一步讨论。

最后，我们展示使用 20 newsgroup 数据集（一个包含 18846 个文档的集合，使用 sklearn 的 CountVectorizer 进行转换）生成的嵌入。

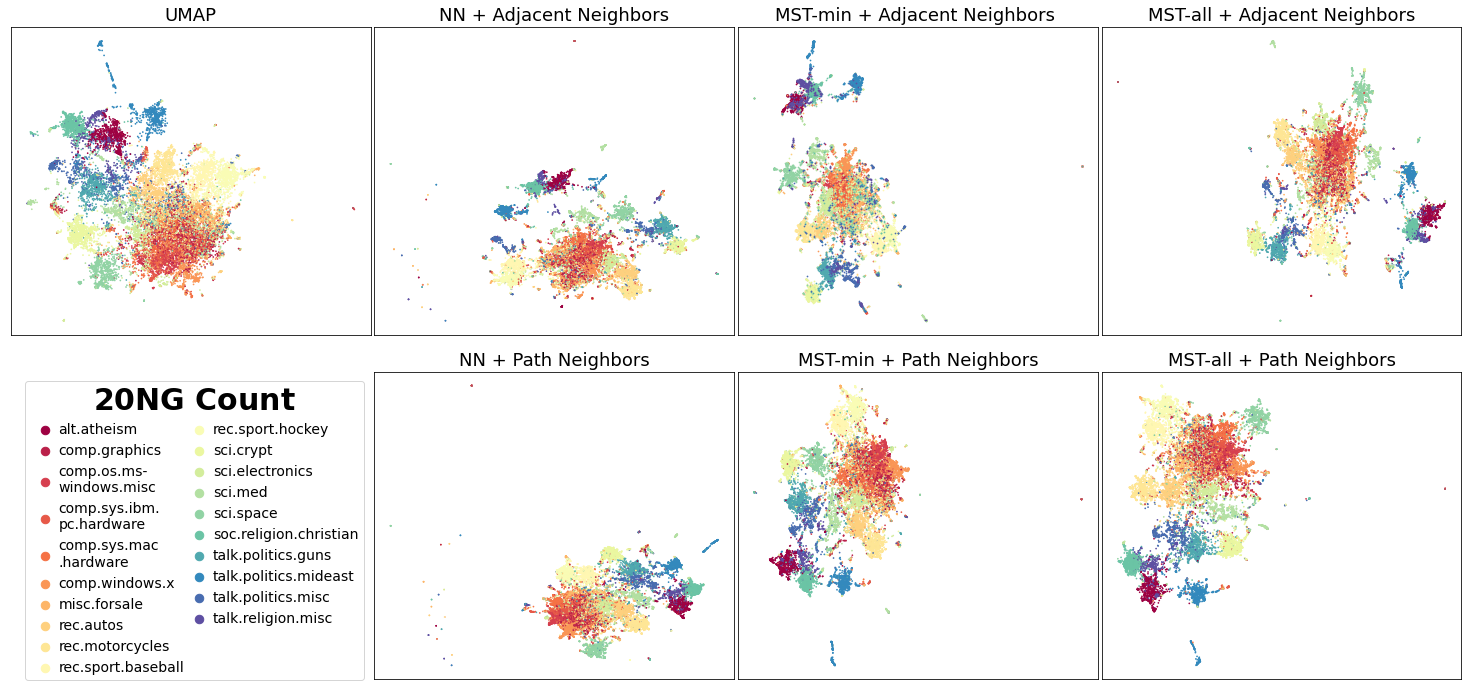
_images/mutual_nn_umap_20ngc.png

我们可以看到，在相似主题（如休闲 (rec) 主题）之间有更好的区分。

从视觉上看，使用 Adjacent Neighbors 和 MST-min 生成的向量产生了分散的密集点簇，例如 FMNIST 中的鞋类类别和 20 NG 中的休闲主题。然而，对于 Path Neighbors，属于同一类别的点组分布更不分散。这是因为 Adjacent Neighbors 不能保证每个局部邻域都有 k 个连通邻居。邻域较小的点将主要接近少数相邻邻居，并被推离其他点更远。

为了定量评估这些方法，作者比较了生成的低维向量的聚类性能。下方显示了执行 KMeans 后的标准化互信息 NMI 结果（有关更多结果信息，请参阅完整论文）。

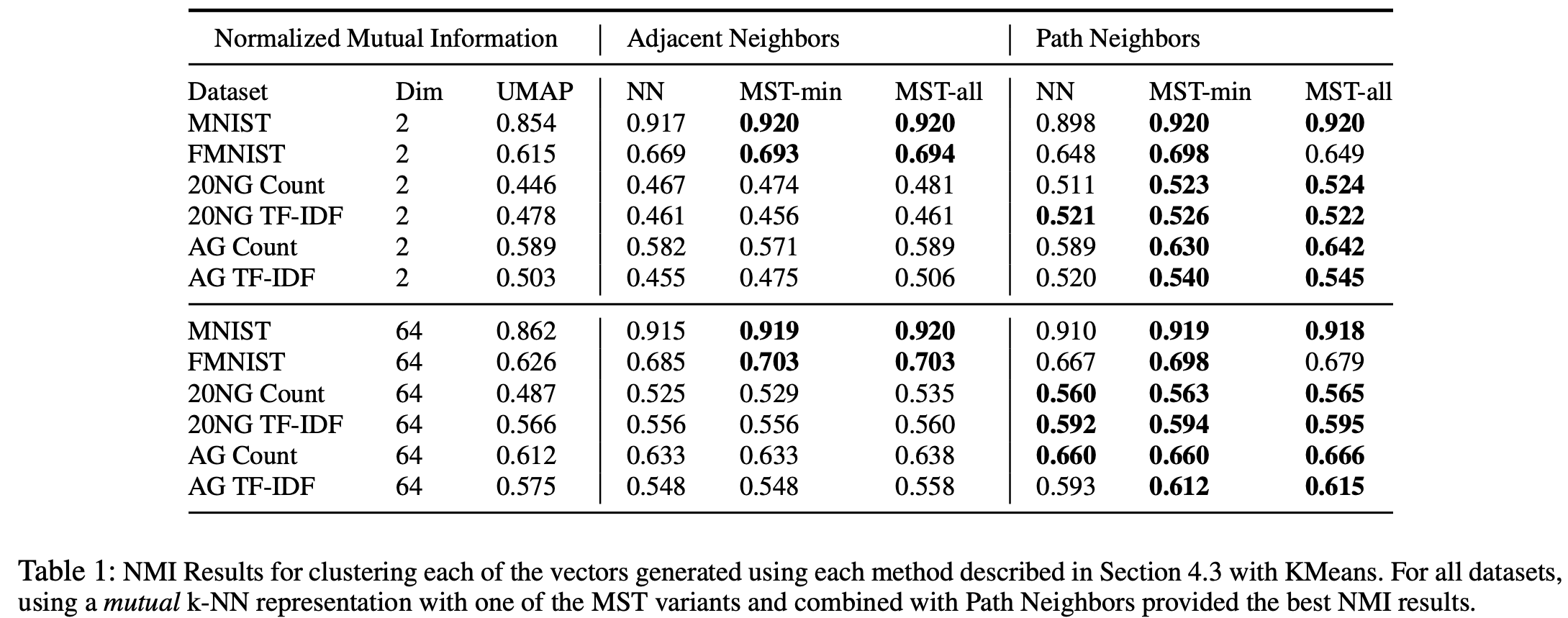
_images/mutual_nn_umap_results.png

这些定量实验表明，MST 变体与 Path Neighbors 结合可以帮助产生更好的聚类结果，以及加权连通图的初始化对于像 UMAP 这样的基于拓扑的降维方法的成功至关重要。

引用我们的工作

如果您在您的工作中使用此实现或引用这些结果，请引用此论文。

@article{Dalmia2021UMAPConnectivity,
  author={Ayush Dalmia and Suzanna Sia},
  title={Clustering with {UMAP:} Why and How Connectivity Matters},
  journal={CoRR},
  volume={abs/2108.05525},
  year={2021},
  url={https://arxiv.org/abs/2108.05525},
  eprinttype={arXiv},
  eprint={2108.05525},
  timestamp={Wed, 18 Aug 2021 19:45:42 +0200},
  biburl={https://dblp.org/rec/journals/corr/abs-2108-05525.bib},
  bibsource={dblp computer science bibliography, https://dblp.org}
  }