如何使用 UMAP
UMAP 是一种通用的流形学习和降维算法。它被设计为与 scikit-learn 兼容,使用了相同的 API,并且能够添加到 sklearn 的 pipeline 中。如果您已经熟悉 sklearn,您应该能够将 UMAP 作为 t-SNE 和其他降维类的直接替代品。如果您对 sklearn 不太熟悉,本教程将逐步引导您了解使用 UMAP 转换和可视化数据的基本知识。
首先,我们需要导入一些有用的工具。显然我们需要 numpy,但我们也会使用 sklearn 中可用的一些数据集,以及 train_test_split 函数来分割数据。最后,我们需要一些绘图工具(matplotlib 和 seaborn)来帮助我们可视化 UMAP 的结果,以及 pandas 使这项工作更容易一些。
import numpy as np
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
%matplotlib inline
sns.set(style='white', context='notebook', rc={'figure.figsize':(14,10)})
企鹅数据

下一步是获取一些数据来处理。为了方便入门,我们将从 企鹅数据集 开始。它不太代表真实世界的数据,但它在数据点数量和特征数量上都很小,这将让我们了解降维正在做什么。
penguins = pd.read_csv("https://raw.githubusercontent.com/allisonhorst/palmerpenguins/c19a904462482430170bfe2c718775ddb7dbb885/inst/extdata/penguins.csv")
penguins.head()
| 物种 | 岛屿 | 喙长_毫米 | 喙深_毫米 | 鳍长_毫米 | 体重_克 | 性别 | 年份 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 阿德利企鹅 | 托格森岛 | 39.1 | 18.7 | 181.0 | 3750.0 | 雄性 | 2007 |
| 1 | 阿德利企鹅 | 托格森岛 | 39.5 | 17.4 | 186.0 | 3800.0 | 雌性 | 2007 |
| 2 | 阿德利企鹅 | 托格森岛 | 40.3 | 18.0 | 195.0 | 3250.0 | 雌性 | 2007 |
| 3 | 阿德利企鹅 | 托格森岛 | NaN | NaN | NaN | NaN | NaN | 2007 |
| 4 | 阿德利企鹅 | 托格森岛 | 36.7 | 19.3 | 193.0 | 3450.0 | 雌性 | 2007 |
由于这是演示目的,我们将去掉数据中的 NaN 值;在实际应用中,应该更仔细地处理缺失数据。
penguins = penguins.dropna()
penguins.species.value_counts()
Adelie 146
Gentoo 119
Chinstrap 68
Name: species, dtype: int64

有关数据集本身的更多详细信息,请参阅 GitHub 存储库。它包含对三种企鹅物种的喙(吻峰)、鳍和体重的测量,以及一些关于企鹅的其他元数据。总共有 333 只不同的企鹅进行了测量。可视化这些数据有点棘手,因为我们不容易绘制 4 维数据。幸运的是,四维并不算大,所以我们可以只做一个成对特征的散点图矩阵来了解情况。Seaborn 可以轻松做到这一点。
sns.pairplot(penguins.drop("year", axis=1), hue='species');
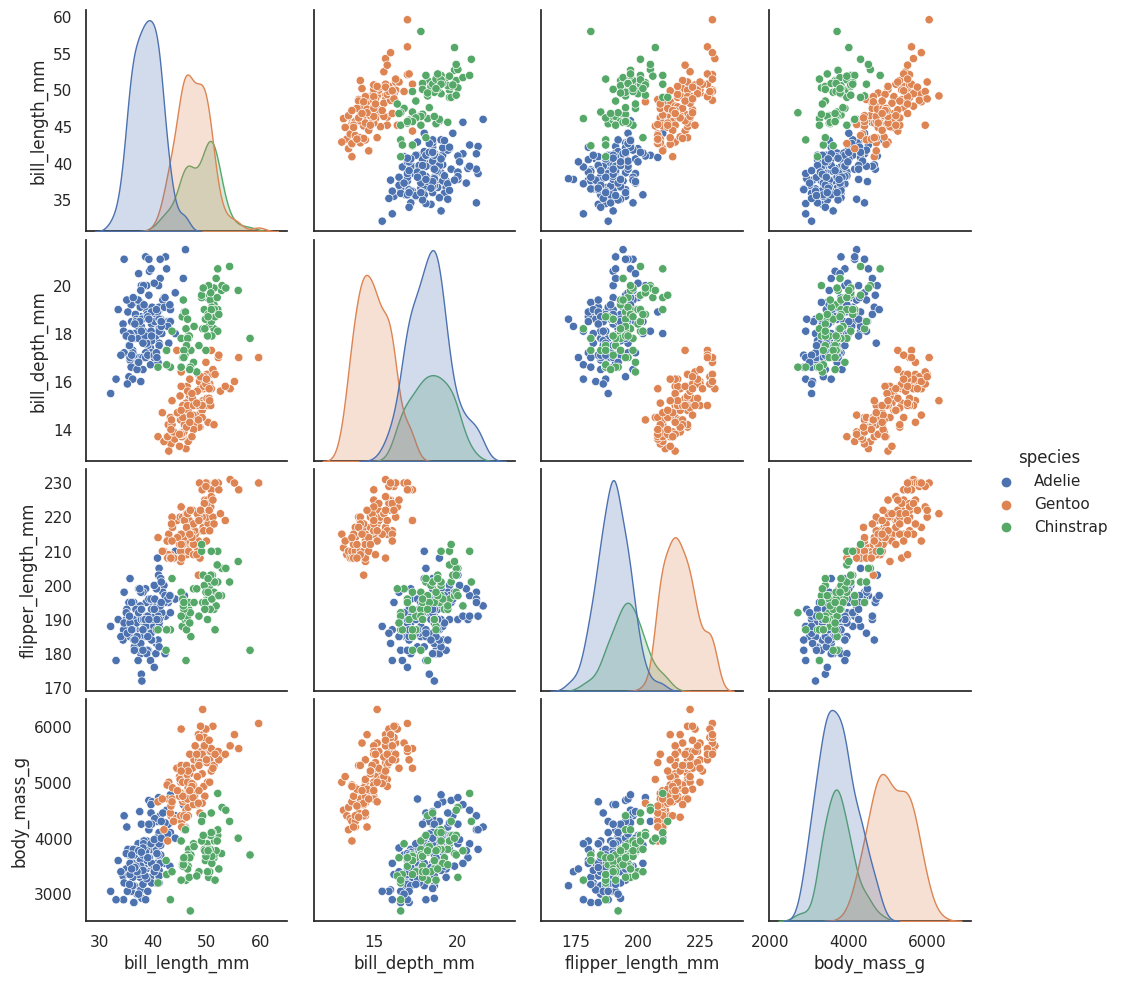
这让我们通过提供数据的所有 2D 视图,对数据的外观有了一些概念。四维足够低,我们可以(某种程度上)在脑海中重构出全维数据是什么样的。既然我们大致知道我们在看什么,问题是像 UMAP 这样的降维技术能为我们做什么?通过以尽可能保留数据结构的方式降低维度,我们可以得到数据的可视化表示,从而使我们能够“看到”数据及其结构,并开始对数据本身获得一些直觉。
要使用 UMAP 完成这项任务,我们首先需要构建一个将为我们工作的 UMAP 对象。这就像实例化类一样简单。所以让我们导入 umap 库并进行实例化。
import umap
reducer = umap.UMAP()
在我们开始处理数据之前,稍微清理一下数据会有所帮助。我们不需要 NaN 值,我们只需要测量列,并且由于测量值完全不同尺度,将每个特征转换为 z-scores(与均值的标准差个数)以便比较会很有帮助。
penguin_data = penguins[
[
"bill_length_mm",
"bill_depth_mm",
"flipper_length_mm",
"body_mass_g",
]
].values
scaled_penguin_data = StandardScaler().fit_transform(penguin_data)
现在我们需要训练我们的降维器,让它了解流形。为此,UMAP 遵循 sklearn API,有一个 fit 方法,我们将要模型学习的数据传递给它。最终,我们将会需要数据的降维表示,所以我们将改为使用 fit_transform 方法,该方法首先调用 fit,然后以 numpy 数组的形式返回转换后的数据。
embedding = reducer.fit_transform(scaled_penguin_data)
embedding.shape
(333, 2)
结果是一个包含 333 个样本的数组,但只有两列特征(而不是我们开始时的四列)。这是因为 UMAP 默认将维度降至 2D。数组的每一行都是相应企鹅的 2 维表示。因此,我们可以将 embedding 绘制成标准的散点图,并根据目标数组着色(因为它适用于转换后的数据,其顺序与原始数据相同)。
plt.scatter(
embedding[:, 0],
embedding[:, 1],
c=[sns.color_palette()[x] for x in penguins.species.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})])
plt.gca().set_aspect('equal', 'datalim')
plt.title('UMAP projection of the Penguin dataset', fontsize=24);
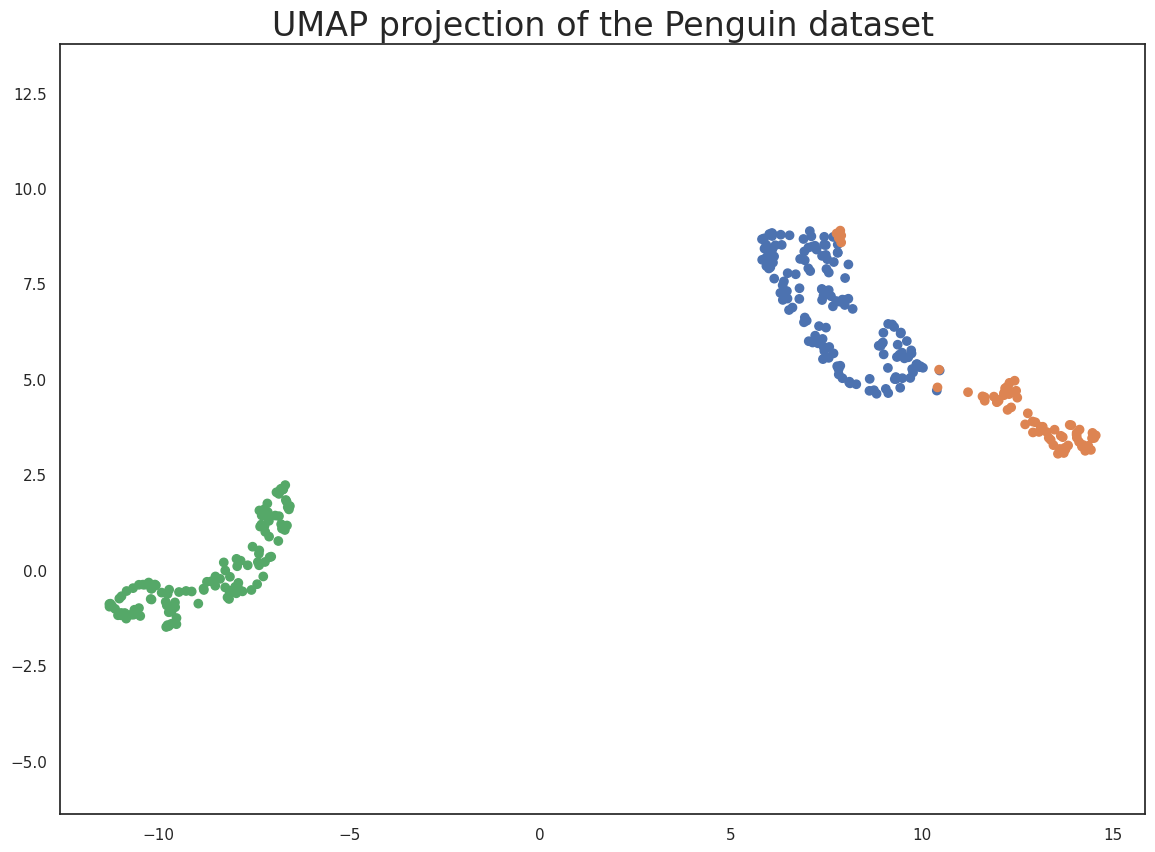
这很好地捕获了数据的结构,并且从散点图矩阵中可以看出,这是相对准确的。当然,我们至少从散点图矩阵中学到了这么多——我们可以这样做,因为我们只有四个不同的维度需要分析。如果我们的数据维度更多,散点图矩阵很快就会变得难以绘制,并且更难解释。因此,从企鹅数据集继续,让我们考虑手写数字数据集。
手写数字数据
首先我们将从 sklearn 加载数据集。
digits = load_digits()
print(digits.DESCR)
.. _digits_dataset:
Optical recognition of handwritten digits dataset
--------------------------------------------------
Data Set Characteristics:
:Number of Instances: 5620
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
.. topic:: References
- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
Graduate Studies in Science and Engineering, Bogazici University.
- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
Linear dimensionalityreduction using relevance weighted LDA. School of
Electrical and Electronic Engineering Nanyang Technological University.
2005.
- Claudio Gentile. A New Approximate Maximal Margin Classification
Algorithm. NIPS. 2000.
我们可以绘制一些图像来了解我们正在看什么。这只需 matplotlib 构建一个轴网格,然后循环遍历它们,依次在每个轴中绘制一张图像。
fig, ax_array = plt.subplots(20, 20)
axes = ax_array.flatten()
for i, ax in enumerate(axes):
ax.imshow(digits.images[i], cmap='gray_r')
plt.setp(axes, xticks=[], yticks=[], frame_on=False)
plt.tight_layout(h_pad=0.5, w_pad=0.01)

正如您所见,这些图像的分辨率相当低——大多数情况下它们可以识别为数字,但也存在一些模糊到即使人类也难以辨认的情况。零是最容易辨识的,明显不同且清晰可辨。除此之外,事情变得稍微困难:一些挤压的八看起来很像一,一些三在写得很糟糕时开始看起来有点像带横杠的七,等等。
每张图像都可以展开成一个长度为 64 的灰度值向量。正是这些 64 维向量是我们希望分析的:我们能辨别出多少数字的结构?至少原则上,64 维对于这项任务来说是多余的,我们可以合理地期望存在一些更少数量的“潜在”特征,这些特征足以很好地描述数据。我们可以尝试一个散点图矩阵——在这种情况下只绘制前 10 维,这样至少可以绘制出来,但正如您很快就能看到的那样,这种方法对于这些数据来说是不够的。
digits_df = pd.DataFrame(digits.data[:,1:11])
digits_df['digit'] = pd.Series(digits.target).map(lambda x: 'Digit {}'.format(x))
sns.pairplot(digits_df, hue='digit', palette='Spectral');
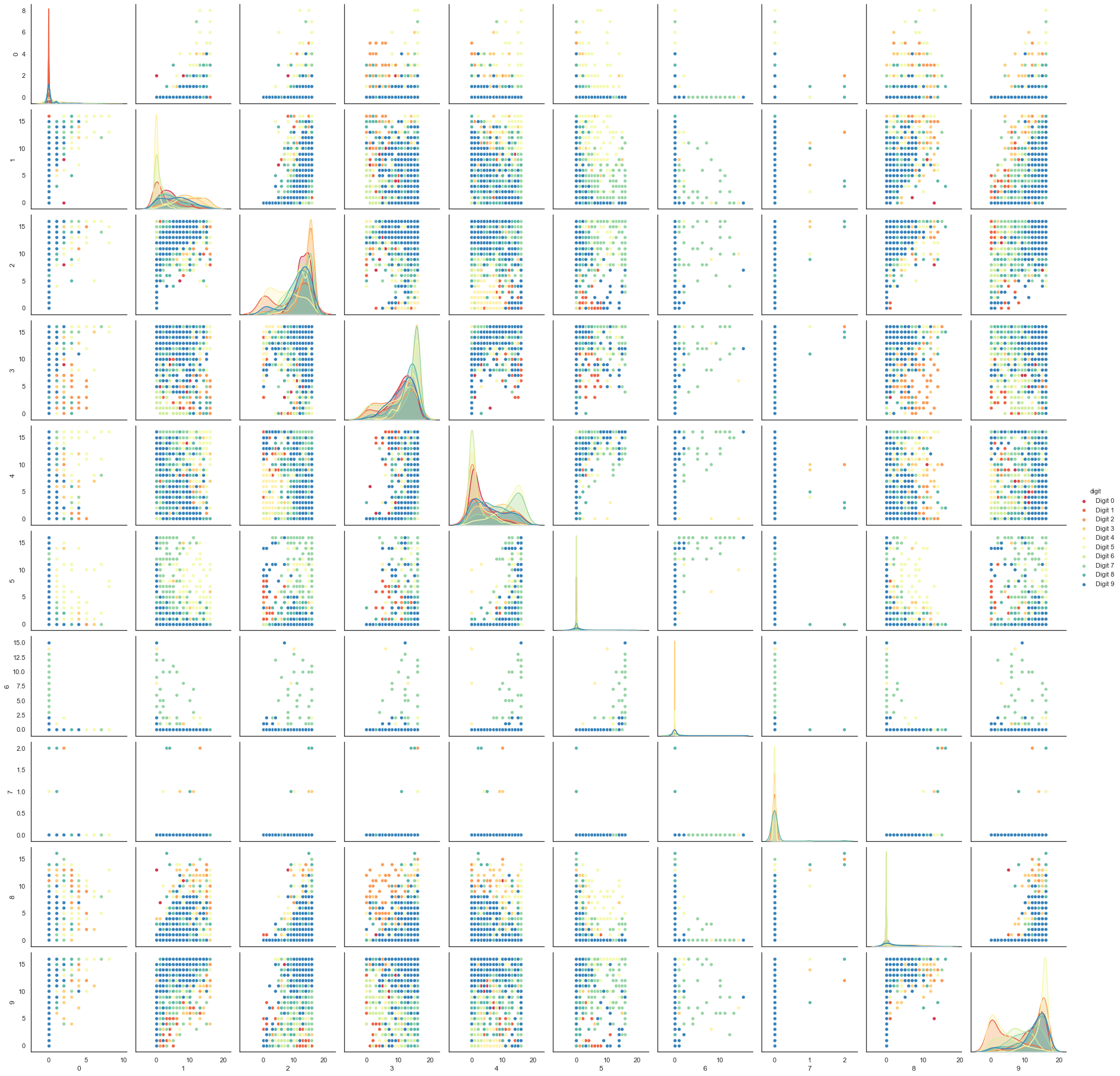
相比之下,我们可以再次尝试使用 UMAP。它的工作原理与之前完全相同:构建模型,训练模型,然后查看转换后的数据。为了展示 UMAP 的更多功能,这次我们将以不同的方式进行,只使用 fit 方法,而不是我们在企鹅数据上使用的 fit_transform 方法。
reducer = umap.UMAP(random_state=42)
reducer.fit(digits.data)
UMAP(a=None, angular_rp_forest=False, b=None,
force_approximation_algorithm=False, init='spectral', learning_rate=1.0,
local_connectivity=1.0, low_memory=False, metric='euclidean',
metric_kwds=None, min_dist=0.1, n_components=2, n_epochs=None,
n_neighbors=15, negative_sample_rate=5, output_metric='euclidean',
output_metric_kwds=None, random_state=42, repulsion_strength=1.0,
set_op_mix_ratio=1.0, spread=1.0, target_metric='categorical',
target_metric_kwds=None, target_n_neighbors=-1, target_weight=0.5,
transform_queue_size=4.0, transform_seed=42, unique=False, verbose=False)
现在,我们不再返回嵌入结果,而是直接获取 reducer 对象,它现在已经在我们传递给它的数据集上进行了训练。要访问生成的转换结果,我们可以查看 reducer 对象的 embedding_ 属性,或者在原始数据上调用 transform 方法。
embedding = reducer.transform(digits.data)
# Verify that the result of calling transform is
# idenitical to accessing the embedding_ attribute
assert(np.all(embedding == reducer.embedding_))
embedding.shape
(1797, 2)
现在我们有了一个包含 1797 行(每个手写数字样本一行)但只有 2 列的数据集。与企鹅示例一样,我们现在可以绘制生成的嵌入结果,并根据数据点所属的类别(即它们代表的数字)进行着色。
plt.scatter(embedding[:, 0], embedding[:, 1], c=digits.target, cmap='Spectral', s=5)
plt.gca().set_aspect('equal', 'datalim')
plt.colorbar(boundaries=np.arange(11)-0.5).set_ticks(np.arange(10))
plt.title('UMAP projection of the Digits dataset', fontsize=24);
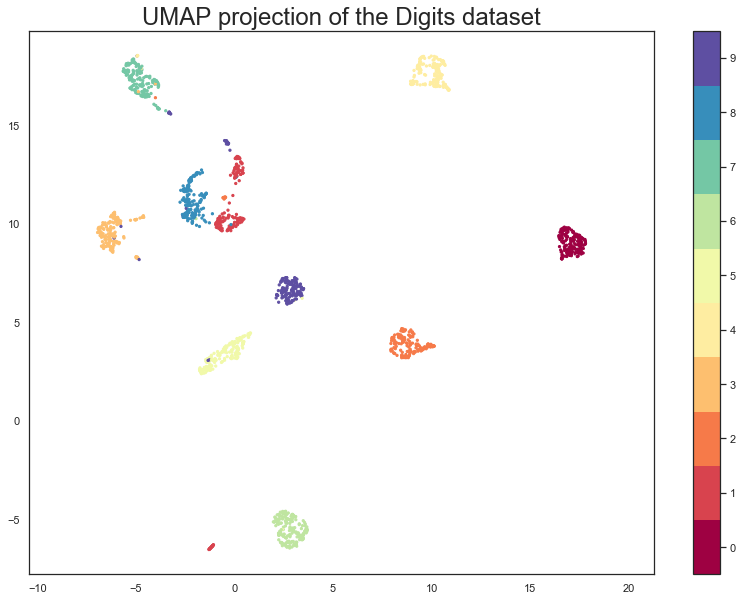
我们看到 UMAP 成功捕获了数字类别。也存在一些有趣的现象,某些数字类别相互融合(参见八、一和七,中间夹杂着一些九),也有一些数字被明确推开,表现得明显不同(右侧的零、顶部的四,以及底部一的小聚类)。为了更好地理解 UMAP 为什么会这样做,查看实际涉及的数字会很有帮助。可以使用 bokeh 并使用鼠标悬停工具提示查看图像来做到这一点。
首先,我们需要对所有图像进行编码,以便包含在 dataframe 中。
from io import BytesIO
from PIL import Image
import base64
def embeddable_image(data):
img_data = 255 - 15 * data.astype(np.uint8)
image = Image.fromarray(img_data, mode='L').resize((64, 64), Image.Resampling.BICUBIC)
buffer = BytesIO()
image.save(buffer, format='png')
for_encoding = buffer.getvalue()
return 'data:image/png;base64,' + base64.b64encode(for_encoding).decode()
接下来,我们需要加载 bokeh 和生成合适的交互式绘图所需的各种工具。
from bokeh.plotting import figure, show, output_notebook
from bokeh.models import HoverTool, ColumnDataSource, CategoricalColorMapper
from bokeh.palettes import Spectral10
output_notebook()
最后,我们生成绘图本身,并带有一个自定义的悬停工具提示,其中嵌入了相关数字的图像以及该数字实际所属的类别(这对于即使人类也很难正确分类的数字非常有用)。
digits_df = pd.DataFrame(embedding, columns=('x', 'y'))
digits_df['digit'] = [str(x) for x in digits.target]
digits_df['image'] = list(map(embeddable_image, digits.images))
datasource = ColumnDataSource(digits_df)
color_mapping = CategoricalColorMapper(factors=[str(9 - x) for x in digits.target_names],
palette=Spectral10)
plot_figure = figure(
title='UMAP projection of the Digits dataset',
width=600,
height=600,
tools=('pan, wheel_zoom, reset')
)
plot_figure.add_tools(HoverTool(tooltips="""
<div>
<div>
<img src='@image' style='float: left; margin: 5px 5px 5px 5px'/>
</div>
<div>
<span style='font-size: 16px; color: #224499'>Digit:</span>
<span style='font-size: 18px'>@digit</span>
</div>
</div>
"""))
plot_figure.scatter(
'x',
'y',
source=datasource,
color=dict(field='digit', transform=color_mapping),
line_alpha=0.6,
fill_alpha=0.6,
size=4
)
show(plot_figure)
可以看出,融合在一和七之间的九是形状奇特的九(它们不太圆),而且确实在一(带帽)和带横杠的七之间出人意料地良好地插值。相比之下,绘图底部一的小的离散聚类是由带脚的一(底部有一条水平线)组成的,它们确实与整体的一群有很大的区别。
至此,我们对 UMAP 的基本用法进行了介绍——希望这能为您自己开始使用提供帮助。当您希望更深入地了解时,还可以获得涵盖 UMAP 参数和更高级用法的进一步教程。
企鹅数据信息
企鹅数据来自
Gorman KB, Williams TD, Fraser WR (2014) Antarctic Penguins (Genus Pygoscelis) 群落内的生态性别二态性与环境变异性。PLoS ONE 9(3): e90081。doi:10.1371/journal.pone.0090081
在此处查看全文HERE。
原始数据访问和使用
Gorman 等人写道:“此处报告的数据可在 PAL-LTER 数据系统(数据集 #219、220 和 221)公开获取:http://oceaninformatics.ucsd.edu/datazoo/data/pallter/datasets。这些数据也保存在美国 (US) LTER Network 的信息系统数据门户中:https://portal.lternet.edu/。因此,有兴趣使用这些数据的个人应遵守美国 LTER Network 的数据访问政策、要求和使用协议:https://lternet.edu/data-access-policy/。”
任何有兴趣发表这些数据的人都应联系 Kristen Gorman 博士,讨论分析事宜并合作完成任何最终产品。
企鹅图片作者:Alison Horst。