合并多个 UMAP 模型
可以将多个 UMAP 模型组合在一起,前提是它们基于相同的基础数据运行。为了了解这是如何工作的,回顾一下 UMAP 使用中间的模糊拓扑表示(参见UMAP 工作原理)。给定相同基础数据的不同视图,这将生成不同的模糊拓扑表示。我们可以对这些表示应用交集或并集,得到一个新的复合模糊拓扑表示,然后我们可以按照标准的 UMAP 方式将其嵌入低维空间。关键是,为了能够合理地对这些表示进行交集或并集,来自两个不同视图的数据样本之间必须存在一对一的对应关系。
为了了解这是如何工作的,通过实践来看它是很有用的。让我们加载一些库并开始。
import sklearn.datasets
from sklearn.preprocessing import RobustScaler
import seaborn as sns
import pandas as pd
import numpy as np
import umap
import umap.plot
MNIST 数字示例
首先,让我们使用一个相对熟悉的数据集——我们在本教程其他部分使用过的 MNIST 数字数据集。数据是手写数字(0到9)的(灰度)28x28像素图像;总共有70,000张这样的图像,每张图像都被展开成一个784个元素的向量。
mnist = sklearn.datasets.fetch_openml("mnist_784")
为了确保我们了解 UMAP 视角下这个数据集是什么样的,我们可以在完整数据集上运行 UMAP。
mapper = umap.UMAP(random_state=42).fit(mnist.data)
umap.plot.points(mapper, labels=mnist.target, width=500, height=500)

为了让问题更有趣,我们将数据集分成两半——不是分成两组各35,000个样本,而是将每张图像切成两半。也就是说,我们将得到70,000个样本,每个样本是手写数字图像的上半部分,以及另外70,000个样本,每个样本是手写数字图像的下半部分。
top = mnist.data[:, :28 * 14]
bottom = mnist.data[:, 28 * 14:]
这有点人为,但它为我们提供了一个示例数据集,其中我们有两种不同的数据视图,我们仍然可以很好地理解它们。实际上,这种情况更有可能发生在存在两个不同的数据收集过程对相同的基础总体进行采样时。在我们的例子中,我们可以简单地将数据重新拼接起来(例如,使用 numpy 数组进行 hstack 操作),但这可能不可行,因为不同的数据视图可能具有不同的尺度或模态。因此,尽管在这种情况下我们可以将数据拼接起来,但我们将假设我们无法做到这一点——这可能是许多现实世界问题的情况。
让我们首先看看 UMAP 在每个数据集上单独运行时会发生什么。我们将从数字的上半部分开始。
top_mapper = umap.UMAP(random_state=42).fit(top)
umap.plot.points(top_mapper, labels=mnist.target, width=500, height=500)
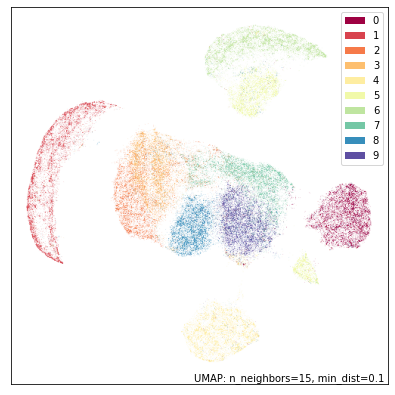
虽然 UMAP 仍然设法大部分分离了不同的数字类别,但我们可以看到结果与在完整标准 MNIST 数据集上运行 UMAP 的结果大相径庭。二和三模糊在一起(正如我们所料,因为我们没有图像的下半部分来区分它们);二和三也与所有八、七和九形成一个大的组(同样,正如我们只看到数字上半部分时所料),而五和六有些区别,但明显彼此相似。只有一、四和零非常清晰可辨。
现在让我们看看用数字下半部分会得到什么样的结果。
bot_mapper = umap.UMAP(random_state=42).fit(bottom)
umap.plot.points(bot_mapper, labels=mnist.target, width=500, height=500)
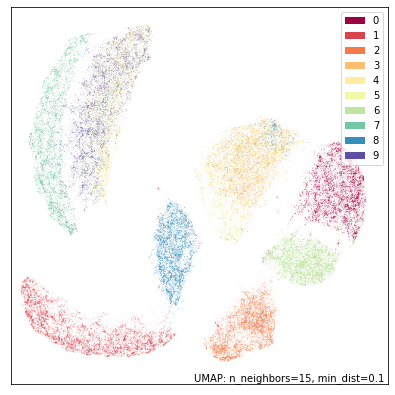
这显然是一个非常不同的数据视图。现在是四和九模糊在一起(大概许多九写成了直线而不是弯曲的笔画),七在附近。二和三彼此非常不同,但三和五合并在一起(正如人们所料,因为下半部分应该看起来相似)。零和六是不同的,但彼此靠近。一、八和二是这个视图中最具特色的数字。
那么,假设我们不能简单地将原始数据粘合在一起并施加合理的度量,我们能做什么?我们可以对模糊拓扑表示进行交集或并集。还需要做一些工作来重新确认 UMAP 的理论假设(局部连通性,近似均匀分布)。幸运的是,只要您手头有拟合好的 UMAP 模型副本(在这种情况下我们有),UMAP 就可以相对容易地做到这一点。要对两个模型进行交集,只需使用*运算符;要对它们进行并集,使用+运算符。请注意,这实际上会花费一些时间,因为我们需要计算组合模型的2D嵌入。
intersection_mapper = top_mapper * bot_mapper
union_mapper = top_mapper + bot_mapper
完成这些后,我们可以可视化结果。首先让我们看看交集。
umap.plot.points(intersection_mapper, labels=mnist.target, width=500, height=500)

正如你所见,虽然这不如完整 MNIST 数据集的 UMAP 绘制效果好,但它很好地恢复了各个数字。剩余重叠最严重的是中心的三和五,它仍然很难完全区分。但请注意,我们也恢复了比两个不同的独立视图更多的整体结构,不同数字类别的布局更接近于在完整数据集上运行 UMAP 的结果。
现在让我们看看并集。
umap.plot.points(union_mapper, labels=mnist.target, width=500, height=500)
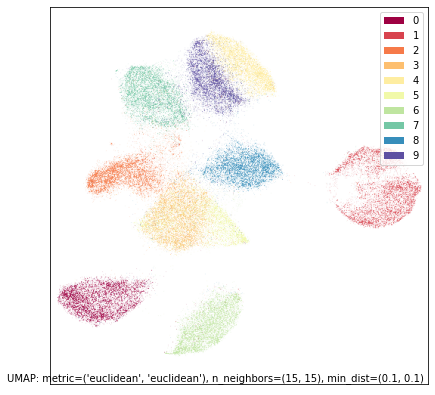
考虑到 UMAP 对最终布局的旋转或反射是不可知的,这基本上与交集的结果相同,因为它几乎是交集结果沿 y 轴的反射。这种结果(交集和并集相似)并非总是如此(事实上这不常见),但由于数字数据集的基础结构如此清晰,我们发现无论从两个半数据集如何将其拼接在一起,都能找到相同的核心基础结构。
如果您愿意尝试一些更具实验性的方法,还有第三种选择,使用-运算符,它有效地与模糊集补集进行交集(因此它不是可交换的,就像-暗示的那样)。这里的目标是试图在与第二个视图对比时,提供数据看起来是什么样子的感觉。
contrast_mapper = top_mapper - bot_mapper
umap.plot.points(contrast_mapper, labels=mnist.target, width=500, height=500)

在这种情况下,结果与只嵌入上半部分的结果没有太大差异,因此对比可能没有像我们希望的那样显示出太多。
钻石数据集示例
现在让我们在另一个数据集上尝试相同的方法,在这个数据集上直接在完整数据集上运行 UMAP 的选项是不可用的。为此,我们将使用钻石数据集。在这个数据集中,每一行代表一颗不同的钻石,并提供给定钻石的重量(克拉)、切工、颜色、净度、尺寸(深度、台面、x、y、z)和价格的详细信息。这些不同因素如何相互作用有些复杂。
diamonds = sns.load_dataset('diamonds')
diamonds.head()
| 克拉 | 切工 | 颜色 | 净度 | 深度 | 台面 | 价格 | x | y | z | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.23 | 理想 (Ideal) | E | SI2 | 61.5 | 55.0 | 326 | 3.95 | 3.98 | 2.43 |
| 1 | 0.21 | 优质 (Premium) | E | SI1 | 59.8 | 61.0 | 326 | 3.89 | 3.84 | 2.31 |
| 2 | 0.23 | 良好 (Good) | E | VS1 | 56.9 | 65.0 | 327 | 4.05 | 4.07 | 2.31 |
| 3 | 0.29 | 优质 (Premium) | I | VS2 | 62.4 | 58.0 | 334 | 4.20 | 4.23 | 2.63 |
| 4 | 0.31 | 良好 (Good) | J | SI2 | 63.3 | 58.0 | 335 | 4.34 | 4.35 | 2.75 |
为了我们的目的,让我们将“价格”作为“目标”变量(在数据集用于机器学习环境时通常如此)。我们希望做的是使用剩余特征提供数据的 UMAP 嵌入。这很棘手,因为我们不能在整个数据集上直接使用欧几里得度量。然而,我们可以做的是将数据分成两种不同的类型:纯粹的数值特征(与尺寸和重量有关)以及分类特征(颜色、切工和净度)。让我们提取这些特征集,以便我们可以独立处理它们。
numeric = diamonds[["carat", "table", "x", "y", "z"]].copy()
ordinal = diamonds[["cut", "color", "clarity"]].copy()
现在我们面临一个新问题:数值特征完全不在同一尺度上,因此任何标准距离度量都将由范围最大的特征主导。我们可以通过进行特征缩放来纠正这个问题。为此,我们将使用 sklearn 的RobustScaler,它使用鲁棒统计量(如中位数和四分位距)对数据特征进行中心化和重缩放。如果我们查看前五行的结果,我们会看到不同的特征现在都相当可比了,并且可以合理地对它们应用欧几里得距离之类的度量。
scaled_numeric = RobustScaler().fit_transform(numeric)
scaled_numeric[:5]
array([[-0.734375 , -0.66666667, -0.95628415, -0.95054945, -0.97345133],
[-0.765625 , 1.33333333, -0.98907104, -1.02747253, -1.07964602],
[-0.734375 , 2.66666667, -0.90163934, -0.9010989 , -1.07964602],
[-0.640625 , 0.33333333, -0.81967213, -0.81318681, -0.79646018],
[-0.609375 , 0.33333333, -0.7431694 , -0.74725275, -0.69026549]])
处理分类特征的最佳方法是什么?如果它们是纯粹的分类特征,将其进行独热编码并使用“Dice”距离是有意义的。这样做的一个缺点是,由于类别很少,这是一个非常粗糙的度量,无法提供太多区分。然而,对于钻石数据集,类别带有严格的顺序:理想切工优于优质切工,优质切工优于非常好切工等等。颜色分级类似,净度也有独特的评级方案。我们可以对这些类别使用序数编码。现在,虽然值的范围可能不同,但它们之间的差异都是可比的——每个等级水平相差1。这意味着我们不需要在序数编码后对这些数据进行重缩放。
ordinal["cut"] = ordinal.cut.map({"Fair":0, "Good":1, "Very Good":2, "Premium":3, "Ideal":4})
ordinal["color"] = ordinal.color.map({"D":0, "E":1, "F":2, "G":3, "H":4, "I":5, "J":6})
ordinal["clarity"] = ordinal.clarity.map({"I1":0, "SI2":1, "SI1":2, "VS2":3, "VS1":4, "VVS2":5, "VVS1":6, "IF":7})
ordinal
| 切工 | 颜色 | 净度 | |
|---|---|---|---|
| 0 | 4 | 1 | 1 |
| 1 | 3 | 1 | 2 |
| 2 | 1 | 1 | 4 |
| 3 | 3 | 5 | 3 |
| 4 | 1 | 6 | 1 |
| ... | ... | ... | ... |
| 53935 | 4 | 0 | 2 |
| 53936 | 1 | 0 | 2 |
| 53937 | 2 | 0 | 2 |
| 53938 | 3 | 4 | 1 |
| 53939 | 4 | 0 | 1 |
53940 行 × 3 列
正如前所述,我们可以将欧几里得距离用作重缩放后的数值数据的合理距离度量。另一方面,由于不同的序数类别完全独立,并且我们有严格的序数编码,所谓的“曼哈顿”距离在这里更有意义——它仅仅是每个类别绝对差异的总和。像以前一样,我们现在可以在每个数据集上训练 UMAP 模型——然而,这次由于数据集不同,我们需要不同的度量甚至不同的n_neighbors值。
numeric_mapper = umap.UMAP(n_neighbors=15, random_state=42).fit(scaled_numeric)
ordinal_mapper = umap.UMAP(metric="manhattan", n_neighbors=150, random_state=42).fit(ordinal.values)
我们可以看看这些独立的数据视图使用 UMAP 降维到 2D 的结果。让我们先看看关于钻石尺寸和重量的数值数据。我们可以按价格着色,以了解数据集如何组合在一起。
umap.plot.points(numeric_mapper, values=diamonds["price"], cmap="viridis")
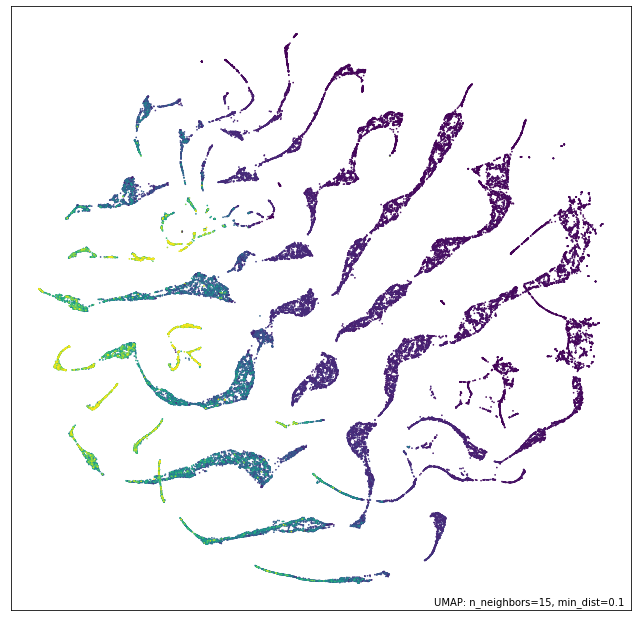
我们看到,虽然数据通常与钻石的价格有所关联,但数据中存在明显不同的分支,大概对应于不同的切工样式,以及这如何根据重量导致钻石在不同维度上产生不同的尺寸。
相比之下,我们可以看看序数数据。在这种情况下,我们也会按不同的类别以及价格进行着色。
fig, ax = umap.plot.plt.subplots(2, 2, figsize=(12,12))
umap.plot.points(ordinal_mapper, labels=diamonds["color"], ax=ax[0,0])
umap.plot.points(ordinal_mapper, labels=diamonds["clarity"], ax=ax[0,1])
umap.plot.points(ordinal_mapper, labels=diamonds["cut"], ax=ax[1,0])
umap.plot.points(ordinal_mapper, values=diamonds["price"], cmap="viridis", ax=ax[1,1])
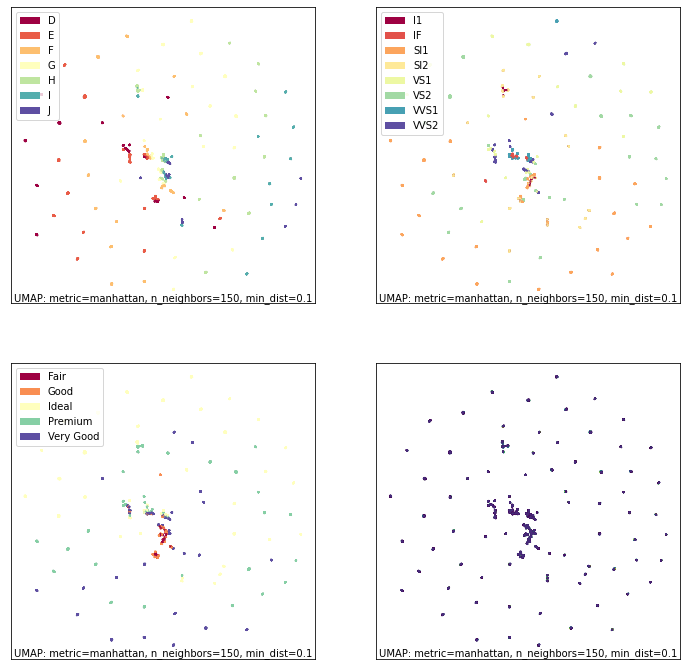
如你所见,这是一个截然不同的结果!序数数据具有相对粗糙的度量,因为不同的类别只能取少量离散值。这意味着,相对于颜色、切工和净度这三方面,钻石要么几乎完全相同,要么区别很大。结果是密度非常高的紧密分组。你可以在图表中看到从左到右的颜色渐变;按切工或净度着色会显示不同的分层。这些非常不同的分层组合在一起,形成了这种高度聚类的嵌入。正是由于这个原因,我们需要如此高的n_neighbors值:数据的局部结构仅仅是相同类别的簇;我们需要看到更远的结构才能学到更多。
考虑到这些截然不同的数据视图,如果我们尝试将它们集成在一起会得到什么?像之前一样,我们可以使用交集和并集运算符简单地组合模型。如前所述,这是一个相当耗时的操作,因为需要优化组合模型的新 2D 表示。
intersection_mapper = numeric_mapper * ordinal_mapper
union_mapper = numeric_mapper + ordinal_mapper
让我们先看看交集;在这里,我们只真正降低了连通性,因为边的分配概率是它们在两个数据视图中都存在(在重新确认局部连通性和均匀分布假设之前)。
umap.plot.points(intersection_mapper, values=diamonds["price"], cmap="viridis")

我们得到的结果最接近于数值数据视图。为什么会这样?因为分类数据视图中的点要么是确切连接的(因为它们相同或几乎相同),要么是非常松散的。以接近确定性连接的点是非常密集的簇——图中的几乎是点——而我们通过交集所做的主要是用数值数据提供的更精细、更多变的连通性来打破这些簇。同时,我们已经将结果从单独的数值数据视图显著移开;分类信息使得每个簇的价格更加均匀(而不是梯度变化)。
鉴于此结果,您对并集有何预期?
umap.plot.points(union_mapper, labels=diamonds["color"])
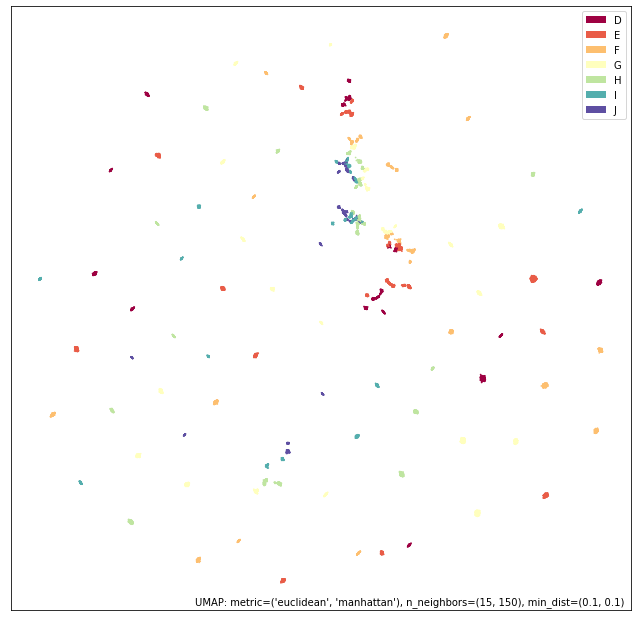
我们在实践中得到的结果更像是数据的分类视图。这次我们只增加了连通性(在重新确认局部连通性和均匀分布假设之前);因此,我们保留了高连通性分类视图的大部分结构。然而请注意,我们在图表的中心创建了更多连接和连贯的簇,显示了各种钻石颜色,并且引入的数值尺寸和重量信息导致了边缘单个簇的重新排列。
我们可以更进一步,尝试对比组合方法。
contrast_mapper = numeric_mapper - ordinal_mapper
umap.plot.points(contrast_mapper, values=diamonds["price"], cmap="viridis")
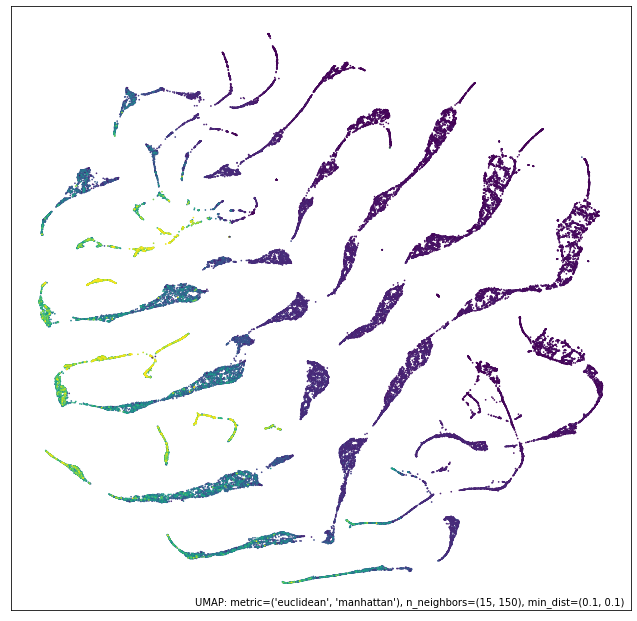
在这里,我们看到我们保留了数值数据视图的大部分结构,但将其进一步细化和分解为清晰的簇,每个簇中都有价格梯度。
为了进一步展示这种方法的强大之处,我们可以更进一步,将数值数据视图基于更高的n_neighbors值的嵌入与我们现有数值和分类数据的并集进行交集——提供一个由三个更简单的模型组成的模型。
intersect_union_mapper = umap.UMAP(random_state=42, n_neighbors=60).fit(numeric) * union_mapper
umap.plot.points(intersect_union_mapper, values=diamonds["price"], cmap="viridis")

在这里,较大n_neighbors值带来的更大的全局结构将更长的线条连接在一起,我们得到了一个有趣的结果。在这种情况下,它不一定特别有信息量,但作为一种演示,即使是组合的模型也可以相互组合,叠加潜在的许多不同视图。