嵌入到非欧空间
默认情况下,UMAP 将数据嵌入到欧几里得空间。对于 2D 可视化而言,这意味着数据被嵌入到一个适合散点图的 2D 平面中。然而,实际上并没有任何主要限制阻止该算法在其他更有趣的嵌入空间中工作。在本教程中,我们将探讨如何让 UMAP 嵌入到其他空间中,如何嵌入到您自己的自定义空间中,以及这种方法可能有什么用处。
首先,我们将加载常用的库。在这种情况下,我们将不使用 umap.plot 功能,而是直接使用 matplotlib,因为我们将为一些更独特的嵌入空间生成自定义可视化效果。
import numpy as np
import numba
import sklearn.datasets
import matplotlib.pyplot as plt
import seaborn as sns
from mpl_toolkits.mplot3d import Axes3D
import umap
%matplotlib inline
sns.set(style='white', rc={'figure.figsize':(10,10)})
作为测试数据集,我们将使用 sklearn 中的 PenDigits 数据集——嵌入到奇异空间中可能计算量更大,因此一个相对较小的数据集会很有用。
digits = sklearn.datasets.load_digits()
平面嵌入
简单的平面嵌入已经足够简单了——这是 UMAP 的默认设置。在这里,我们将再次运行这个示例,以确保您熟悉它是如何工作的,以及在平面中嵌入的简单情况下,PenDigits 数据集的 UMAP 嵌入结果是什么样的。
plane_mapper = umap.UMAP(random_state=42).fit(digits.data)
plt.scatter(plane_mapper.embedding_.T[0], plane_mapper.embedding_.T[1], c=digits.target, cmap='Spectral')
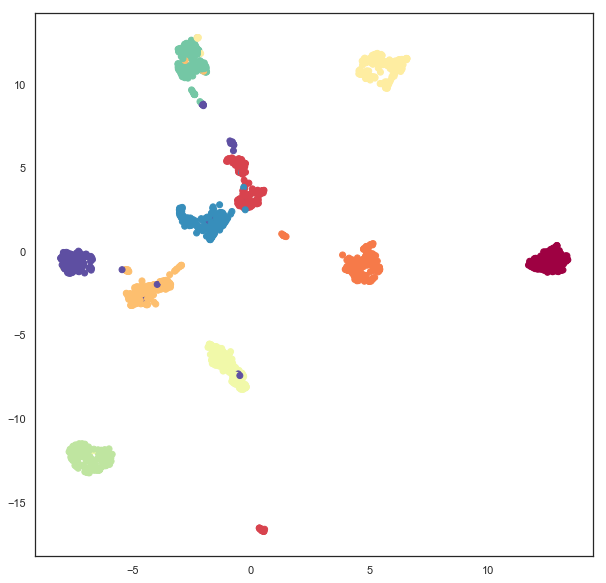
球面嵌入
如果我们想将数据嵌入到球面上而不是平面上怎么办?例如,如果我们有理由预期某种周期性行为,或者由于其他原因预期没有一个点可以无限远离任何其他点,那么这样做可能是有意义的。要让 UMAP 嵌入到球面上,我们需要使用 output_metric 参数,该参数指定用于输出空间的度量标准。默认情况下,UMAP 使用欧几里得 output_metric(甚至对此情况有特殊的更快代码路径),但您可以传入其他度量标准。UMAP 支持的度量标准之一是 Haversine 度量,用于测量球体上的距离,以纬度和经度(弧度)表示。如果我们将 output_metric 设置为 "haversine",那么 UMAP 将使用它来测量嵌入空间中的距离。
sphere_mapper = umap.UMAP(output_metric='haversine', random_state=42).fit(digits.data)
结果是将 pendigits 数据相对于球体上的 Haversine 距离进行嵌入。问题在于,如果我们天真地进行可视化,就会得到毫无意义的结果。
plt.scatter(sphere_mapper.embedding_.T[0], sphere_mapper.embedding_.T[1], c=digits.target, cmap='Spectral')
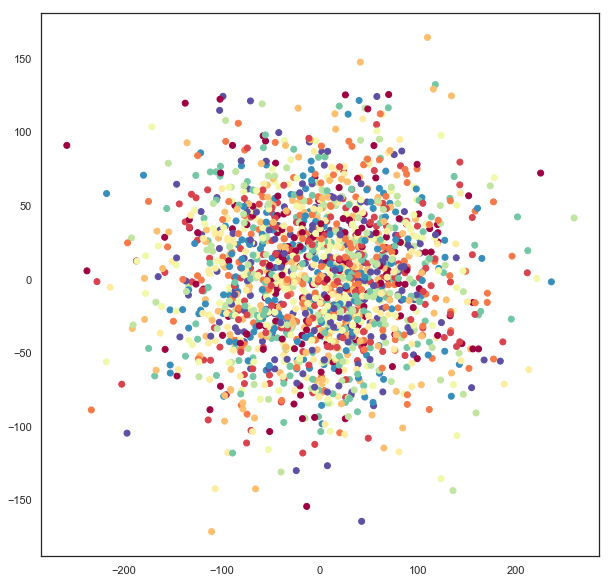
出错的地方在于,在嵌入距离度量下,点 \((0, \pi)\) 与点 \((0, 3\pi)\) 的距离为零,因为它将一直绕赤道一周。您会注意到,上面图中 x 轴和 y 轴的比例远远超出了范围 \((-\pi, \pi)\) 和 \((0, 2\pi)\),因此这不是数据的正确表示。但是,我们可以使用简单的公式将这些数据映射到嵌入在 3d 空间中的球体上。
x = np.sin(sphere_mapper.embedding_[:, 0]) * np.cos(sphere_mapper.embedding_[:, 1])
y = np.sin(sphere_mapper.embedding_[:, 0]) * np.sin(sphere_mapper.embedding_[:, 1])
z = np.cos(sphere_mapper.embedding_[:, 0])
现在 x、y 和 z 给出了位于球体表面上每个嵌入点的 3d 坐标。我们可以使用 matplotlib 的 3d 绘图功能对其进行可视化,并看到我们实际上已经将数据合理地嵌入到了球体的表面上。
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=digits.target, cmap='Spectral')
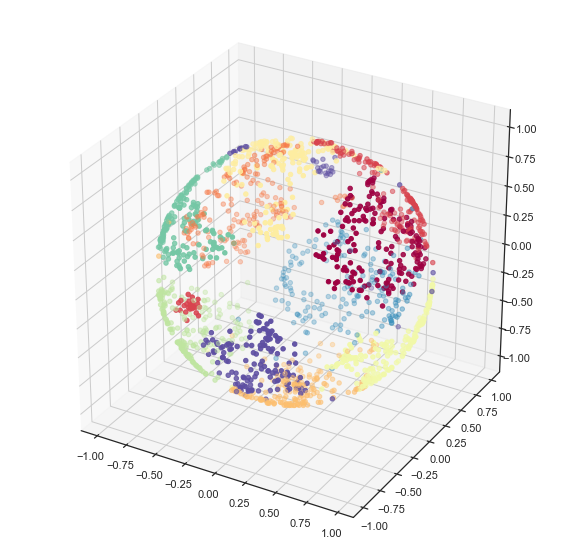
如果您更喜欢 2d 图,我们可以将这些坐标转换为适当范围内的经/纬度坐标,从而得到球体数据的地图投影效果。
x = np.arctan2(x, y)
y = -np.arccos(z)
plt.scatter(x, y, c=digits.target.astype(np.int32), cmap='Spectral')
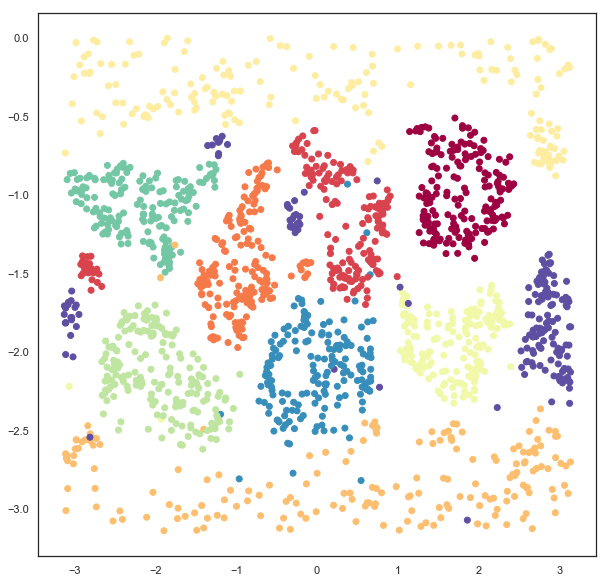
在自定义度量空间中嵌入
如果您对度量空间有其他自定义概念并想将数据嵌入其中怎么办?就像 UMAP 支持为输入数据编写自定义距离度量一样(只要它们可以用 numba 编译),output_metric 参数也可以接受自定义距离函数。一个注意事项是,为了支持梯度下降优化,距离函数需要返回距离以及距离的梯度向量。后一点可能需要用户具备一些微积分知识。第二个注意事项是,以一种没有坐标约束的方式对嵌入空间进行参数化非常有益——否则梯度下降可能会将点移动到嵌入空间之外,导致不良结果。这就是为什么,例如,球体示例只是让点环绕而不是将坐标限制在适当范围内的原因。
让我们看一个构建不同类型空间(环面)距离度量和梯度的例子。环面本质上就像甜甜圈的外表面。我们可以用 x、y 坐标对环面进行参数化,需要注意的是我们可以“环绕”(类似于球体)。在这种模型中,距离主要就是欧几里得距离,我们只需要检查哪个方向更短——穿过还是环绕——并确保我们考虑环绕多次的等价性。我们可以编写一个简单的函数来计算这一点。
@numba.njit(fastmath=True)
def torus_euclidean_grad(x, y, torus_dimensions=(2*np.pi,2*np.pi)):
"""Standard euclidean distance.
..math::
D(x, y) = \sqrt{\sum_i (x_i - y_i)^2}
"""
distance_sqr = 0.0
g = np.zeros_like(x)
for i in range(x.shape[0]):
a = abs(x[i] - y[i])
if 2*a < torus_dimensions[i]:
distance_sqr += a ** 2
g[i] = (x[i] - y[i])
else:
distance_sqr += (torus_dimensions[i]-a) ** 2
g[i] = (x[i] - y[i]) * (a - torus_dimensions[i]) / a
distance = np.sqrt(distance_sqr)
return distance, g/(1e-6 + distance)
注意,梯度仅源自标准欧几里得梯度,我们只需要根据环绕方式检查方向来计算距离。我们现在可以将该函数直接插入到 output_metric 参数中,最终将数据嵌入到环面上。
torus_mapper = umap.UMAP(output_metric=torus_euclidean_grad, random_state=42).fit(digits.data)
与球体情况一样,由于环绕和多次循环的等价性,朴素的可视化看起来会很奇怪。但是,就像环面一样,我们可以通过使用一些简单的几何学知识计算点的 3d 坐标来构建合适的可视化(是的,我还是查了一下以确认)。
R = 3 # Size of the doughnut circle
r = 1 # Size of the doughnut cross-section
x = (R + r * np.cos(torus_mapper.embedding_[:, 0])) * np.cos(torus_mapper.embedding_[:, 1])
y = (R + r * np.cos(torus_mapper.embedding_[:, 0])) * np.sin(torus_mapper.embedding_[:, 1])
z = r * np.sin(torus_mapper.embedding_[:, 0])
现在我们可以使用 matplotlib 对结果进行可视化,并看到数据确实已经适当地嵌入到环面上。
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=digits.target, cmap='Spectral')
ax.set_zlim3d(-3, 3)
ax.view_init(35, 70)
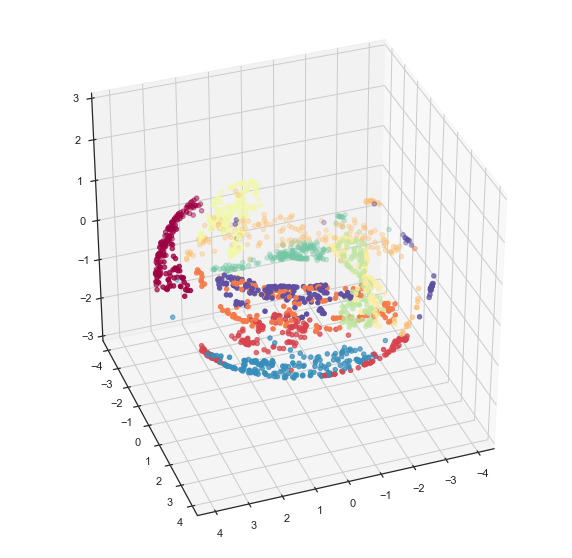
与环面一样,我们可以做一些几何学处理,将环面展开成具有适当边界的平面。
u = np.arctan2(x,y)
v = np.arctan2(np.sqrt(x**2 + y**2) - R, z)
plt.scatter(u, v, c=digits.target, cmap='Spectral')

一个实际示例
虽然到目前为止给出的例子可能有一些用途(因为某些数据确实具有适合在球体或环面中更好地表示的周期性或循环结构),但大多数数据并不真正属于用户可以先验地期望位于奇异流形上的范围。在其他空间中嵌入的能力是否有更实际的用途?事实证明是有的。一个有趣的例子是考虑由 2d 高斯分布形成的空间。我们可以通过两个高斯分布的 PDF 内积的负对数来测量它们之间的距离(两个高斯分布由一个 2d 均值向量和一个给出协方差的 2x2 矩阵参数化),因为这有一个很好的封闭形式解,并且计算起来相当方便。这为我们提供了一个可以嵌入的度量空间,其中样本不是以 2d 中的点表示,而是以 2d 中的高斯分布表示,编码了高维空间中每个样本如何嵌入的不确定性。
当然,我们仍然面临适合 SGD 的参数化问题——要求协方差矩阵是对称正定的很有挑战性。取而代之的是,我们可以用宽度、高度和角度来参数化协方差,并在需要时从中恢复协方差矩阵。这给了我们总共 5 个分量可以嵌入(两个用于均值,三个用于描述协方差的参数)。我们可以简单地做到这一点,因为适当的度量标准已经定义好了。注意,我们必须专门传递 n_components=5,因为我们需要明确地嵌入到 5 维空间中以支持与 2d 高斯分布相关的所有协方差参数。
gaussian_mapper = umap.UMAP(output_metric='gaussian_energy',
n_components=5,
random_state=42).fit(digits.data)
由于我们将数据嵌入到了 5 维空间,可视化不像之前那么简单。我们可以通过只查看均值来开始可视化结果,均值是高斯分布众数的 2d 位置。传统的散点图就足够了。
plt.scatter(gaussian_mapper.embedding_.T[0], gaussian_mapper.embedding_.T[1], c=digits.target, cmap='Spectral')
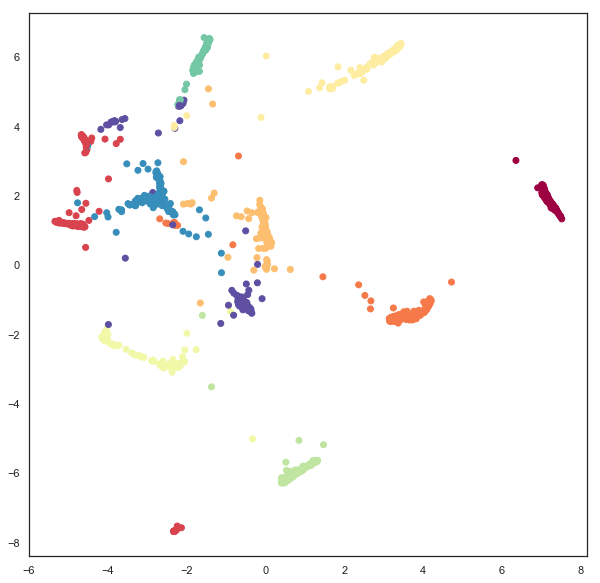
我们看到,我们得到的结果类似于标准欧几里得空间嵌入,但聚类不太清晰,且簇之间有更多的点。为了更清楚地了解发生了什么,需要设计一种方法来显示额外 3 个维度中包含的协方差数据。为此,能够绘制对应于 2d 高斯分布 PDF 超水平集的椭圆将会很有帮助。我们可以从编写一个简单的函数开始,该函数根据位置、宽度、高度和角度(因为这是嵌入计算数据时使用的格式)在图上绘制椭圆。
from matplotlib.patches import Ellipse
def draw_simple_ellipse(position, width, height, angle,
ax=None, from_size=0.1, to_size=0.5, n_ellipses=3,
alpha=0.1, color=None,
**kwargs):
ax = ax or plt.gca()
angle = (angle / np.pi) * 180
width, height = np.sqrt(width), np.sqrt(height)
# Draw the Ellipse
for nsig in np.linspace(from_size, to_size, n_ellipses):
ax.add_patch(Ellipse(position, nsig * width, nsig * height,
angle, alpha=alpha, lw=0, color=color, **kwargs))
现在我们可以通过提供中心点的散点图(像之前一样)来绘制数据,并将其叠加在相关高斯分布的超水平集椭圆上。显而易见的问题是这会导致大量重叠绘制,但这至少提供了一种开始理解我们所产生嵌入的方法。
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111)
colors = plt.get_cmap('Spectral')(np.linspace(0, 1, 10))
for i in range(gaussian_mapper.embedding_.shape[0]):
pos = gaussian_mapper.embedding_[i, :2]
draw_simple_ellipse(pos, gaussian_mapper.embedding_[i, 2],
gaussian_mapper.embedding_[i, 3],
gaussian_mapper.embedding_[i, 4],
ax, color=colors[digits.target[i]],
from_size=0.2, to_size=1.0, alpha=0.05)
ax.scatter(gaussian_mapper.embedding_.T[0],
gaussian_mapper.embedding_.T[1],
c=digits.target, cmap='Spectral', s=3)
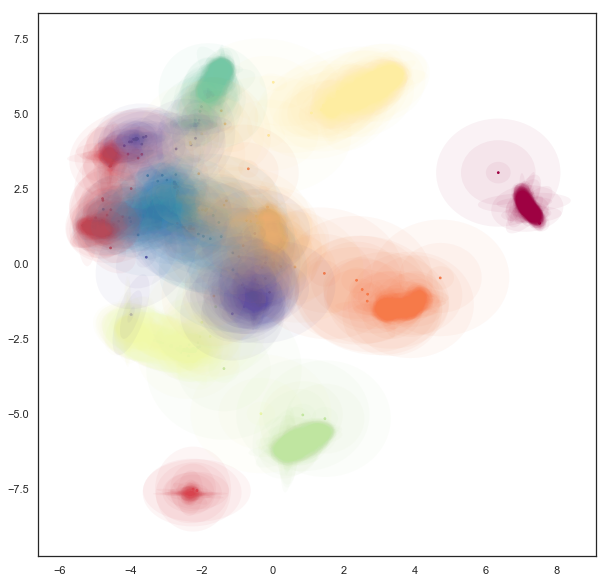
现在我们可以看到,这些点的协方差结构在绝对大小和形状上都有很大的变化。我们注意到,许多落在簇之间的点具有更大的方差,这在某种程度上代表了嵌入位置的更大不确定性。同样值得注意的是,椭圆的形状可以显著变化——有一些非常拉伸的椭圆,与许多非常圆的椭圆截然不同;这在某种程度上代表了不确定性更倾向于沿单线分布,例如。
虽然此图突出显示了离群点的一些协方差结构,但在实践中,这里的重叠绘制掩盖了簇本身许多更有趣的结构。我们可以尝试通过仅绘制每个点一个椭圆并对椭圆使用较低的 alpha 通道值来使其更透明,从而更好地查看此结构。
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111)
for i in range(gaussian_mapper.embedding_.shape[0]):
pos = gaussian_mapper.embedding_[i, :2]
draw_simple_ellipse(pos, gaussian_mapper.embedding_[i, 2],
gaussian_mapper.embedding_[i, 3],
gaussian_mapper.embedding_[i, 4],
ax, n_ellipses=1,
color=colors[digits.target[i]],
from_size=1.0, to_size=1.0, alpha=0.01)
ax.scatter(gaussian_mapper.embedding_.T[0],
gaussian_mapper.embedding_.T[1],
c=digits.target, cmap='Spectral', s=3)

这让我们能够看到簇密度随协方差结构的变化——有些簇始终具有非常紧密的协方差,而另一些簇则更分散(因此在某种意义上具有更大的相关不确定性)。当然,即使在这里我们仍然存在一定程度的重叠绘制,调整 alpha 通道以使其可见将变得越来越困难。相反,我们想要的是一个实际的密度图,显示所有这些高斯分布之和的密度。
为此,我们需要定义一些函数,它们的执行将使用 numba 加速:在给定点评估 2d 高斯分布的密度;评估一个给定点上多个高斯分布之和的密度;以及一个在某个网格中为每个点生成密度(仅对附近的高斯分布求和,以使这种朴素方法更具计算可行性)的函数。
from sklearn.neighbors import KDTree
@numba.njit(fastmath=True)
def eval_gaussian(x, pos=np.array([0, 0]), cov=np.eye(2, dtype=np.float32)):
det = cov[0,0] * cov[1,1] - cov[0,1] * cov[1,0]
if det > 1e-16:
cov_inv = np.array([[cov[1,1], -cov[0,1]], [-cov[1,0], cov[0,0]]]) * 1.0 / det
diff = x - pos
m_dist = cov_inv[0,0] * diff[0]**2 - \
(cov_inv[0,1] + cov_inv[1,0]) * diff[0] * diff[1] + \
cov_inv[1,1] * diff[1]**2
return (np.exp(-0.5 * m_dist)) / (2 * np.pi * np.sqrt(np.abs(det)))
else:
return 0.0
@numba.njit(fastmath=True)
def eval_density_at_point(x, embedding):
result = 0.0
for i in range(embedding.shape[0]):
pos = embedding[i, :2]
t = embedding[i, 4]
U = np.array([[np.cos(t), np.sin(t)], [np.sin(t), -np.cos(t)]])
cov = U @ np.diag(embedding[i, 2:4]) @ U
result += eval_gaussian(x, pos=pos, cov=cov)
return result
def create_density_plot(X, Y, embedding):
Z = np.zeros_like(X)
tree = KDTree(embedding[:, :2])
for i in range(X.shape[0]):
for j in range(X.shape[1]):
nearby_points = embedding[tree.query_radius([[X[i,j],Y[i,j]]], r=2)[0]]
Z[i, j] = eval_density_at_point(np.array([X[i,j],Y[i,j]]), nearby_points)
return Z / Z.sum()
现在我们只需要一个合适的点网格。我们可以使用上面看到的绘图边界,以及出于计算可行性选择的网格大小。numpy 的 meshgrid 函数可以提供实际的网格。
X, Y = np.meshgrid(np.linspace(-7, 9, 300), np.linspace(-8, 8, 300))
现在我们可以使用上面定义的函数来计算网格中每个点上的密度,该密度由嵌入产生的高斯分布给出。
Z = create_density_plot(X, Y, gaussian_mapper.embedding_)
现在我们可以使用 imshow 将结果视为密度图。
plt.imshow(Z, origin='lower', cmap='Reds', extent=(-7, 9, -8, 8), vmax=0.0005)
plt.colorbar()
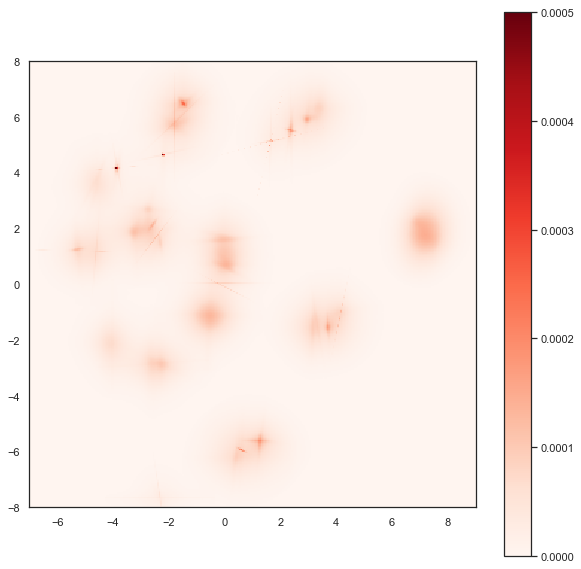
在这里,我们看到了各个簇内的更精细结构,包括一些有趣的线性结构,这表明基于高斯不确定性的嵌入捕获了关于 PenDigits 数据集内部关系的相当详细和有用的信息。
额外内容:在双曲空间中嵌入
作为额外示例,让我们看看如何将数据嵌入到双曲空间中。用于可视化的最流行模型是庞加莱圆盘模型。庞加莱圆盘模型中双曲空间的规则铺砖示例如下所示;您可能会注意到它类似于 M.C. 埃舍尔的著名图像。

理想情况下,我们能够直接嵌入到这个庞加莱圆盘模型中,但实际上这非常困难。问题在于圆盘在其边界半径为一的圆上有一条“无穷远线”。超出这个圆圈,事物就没有很好的定义。您可能还记得关于嵌入到球体和环面的讨论,最好是我们可以对嵌入空间进行参数化,使其难以移出。庞加莱圆盘模型几乎与此相反——一旦我们移出单位圆,我们就离开了流形,进一步的更新将是错误定义的。因此,我们需要双曲空间的一种不同的、约束较少的参数化方法。一种选择是庞加莱上半平面模型,但它同样有一个易于越过的边界。最简单的选择是双曲面模型。在这种模型下,我们可以简单地在 x 和 y 坐标中移动,并在需要计算距离时求解相应的 z 坐标。此模型已在距离度量 "hyperboloid" 下实现,因此我们可以直接使用它。
hyperbolic_mapper = umap.UMAP(output_metric='hyperboloid',
random_state=42).fit(digits.data)
一个简单的可视化选项是直接查看我们得到的 x 和 y 坐标
plt.scatter(hyperbolic_mapper.embedding_.T[0],
hyperbolic_mapper.embedding_.T[1],
c=digits.target, cmap='Spectral')
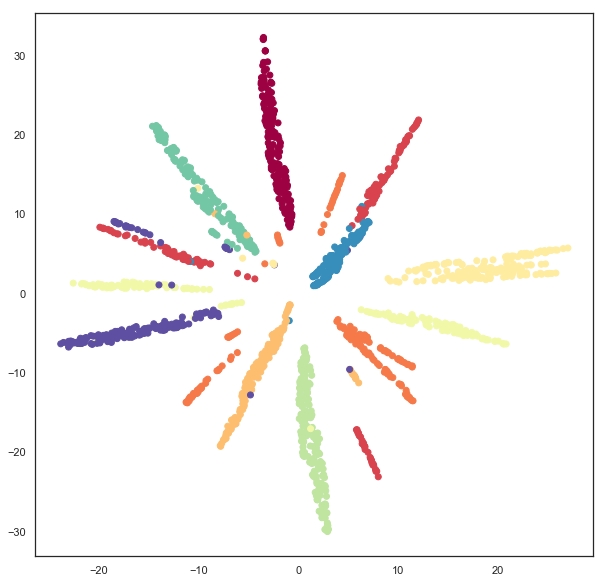
我们还可以求解 z 坐标,并查看数据在 3d 空间中位于双曲面上。
x = hyperbolic_mapper.embedding_[:, 0]
y = hyperbolic_mapper.embedding_[:, 1]
z = np.sqrt(1 + np.sum(hyperbolic_mapper.embedding_**2, axis=1))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=digits.target, cmap='Spectral')
ax.view_init(35, 80)
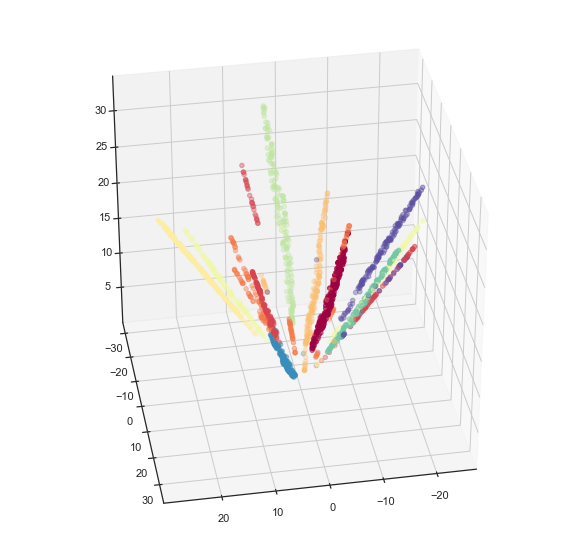
但我们可以做得更多——既然我们已经成功地将数据嵌入到双曲空间中,我们可以将数据映射到庞加莱圆盘模型。这实际上是一个简单的计算。
disk_x = x / (1 + z)
disk_y = y / (1 + z)
现在我们可以按照最初的愿望,在庞加莱圆盘模型嵌入中可视化数据。为此,我们只需生成数据的散点图,然后画出无穷远线的边界圆。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(disk_x, disk_y, c=digits.target, cmap='Spectral')
boundary = plt.Circle((0,0), 1, fc='none', ec='k')
ax.add_artist(boundary)
ax.axis('off');

希望这提供了一个关于如何嵌入到非欧空间的有用示例。最后一个例子理想地突出了这种方法的局限性(我们确实需要一个合适的参数化),以及解决这个问题的一些潜在方法:我们可以对嵌入使用替代参数化,然后将数据转换到所需的表示形式。