使用 UMAP 进行聚类

UMAP 可以作为有效的预处理步骤来提升基于密度聚类的性能。这有点争议，应谨慎尝试。关于其中涉及的一些问题的良好讨论，请参阅 此 stackoverflow 帖子中的各种回答，该帖子讨论了对 t-SNE 结果进行聚类的问题。其中提出的许多令人担忧的点对于对 UMAP 结果进行聚类也同样突出。最值得注意的是，UMAP 与 t-SNE 一样，并不能完全保留密度。UMAP 与 t-SNE 一样，也可能在簇中产生虚假的撕裂，导致聚类结果比数据中实际存在的更细粒度。尽管存在这些担忧，但仍有正当理由将 UMAP 用作聚类的预处理步骤。与任何聚类方法一样，您需要对得出的簇进行一些探索和评估，尽可能尝试验证它们。

话虽如此，让我们通过一个例子来展示聚类方法可能面临的困难，以及 UMAP 如何提供强大的工具来帮助克服这些困难。

首先，我们需要加载一些库。显然我们需要数据，我们可以使用 sklearn 的 fetch_openml 来获取。我们还需要常用的 numpy 和绘图工具。接下来，我们需要 umap 和一些聚类选项。最后，由于我们将使用带标签的数据，我们可以利用强大的聚类评估指标：调整兰德指数 (Adjusted Rand Index) 和 调整互信息 (Adjusted Mutual Information)。

from sklearn.datasets import fetch_openml
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Dimension reduction and clustering libraries
import umap
import hdbscan
import sklearn.cluster as cluster
from sklearn.metrics import adjusted_rand_score, adjusted_mutual_info_score

现在，让我们设置绘图并获取我们将要使用的数据——在本例中是 MNIST 手写数字数据集。MNIST 包含 28x28 像素的手写数字（0 到 9）灰度图像。这些图像可以展开，使得每个数字都可以用一个 784 维向量来描述（图像中每个像素的灰度值）。理想情况下，我们希望聚类能够恢复数字结构。

mnist = fetch_openml('mnist_784', version=1)
mnist.target = mnist.target.astype(int)

为了可视化目的，我们可以使用 UMAP 将数据降至 2 维。当我们在高维空间中对数据进行聚类时，我们可以将聚类结果可视化。然而，首先我们将根据每个数据点所代表的数字来对数据着色——每个数字使用不同的颜色。这将有助于构建接下来的内容。

standard_embedding = umap.UMAP(random_state=42).fit_transform(mnist.data)
plt.scatter(standard_embedding[:, 0], standard_embedding[:, 1], c=mnist.target.astype(int), s=0.1, cmap='Spectral');
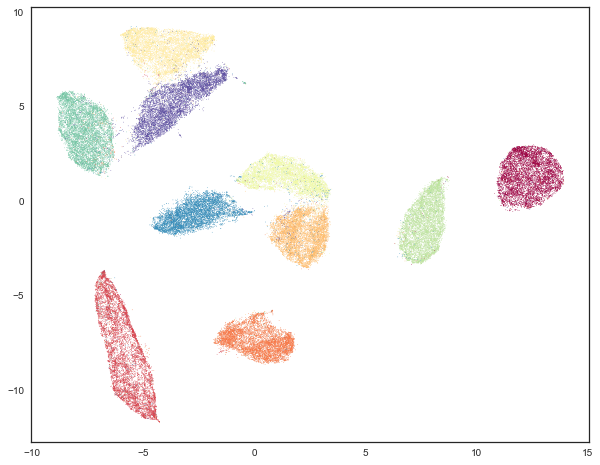
_images/clustering_6_1.png

传统聚类

现在我们希望对数据进行聚类。作为第一次尝试，让我们试试传统方法：K-Means。在这种情况下，我们可以解决 K-Means 聚类的一个难题——选择正确的 k 值，即我们正在寻找的簇的数量。在本例中，我们知道答案是 10。我们将使用 sklearn 的 K-Means 实现，在原始的 784 维数据中寻找 10 个簇。

kmeans_labels = cluster.KMeans(n_clusters=10).fit_predict(mnist.data)

那么聚类效果如何呢？我们可以通过根据簇成员身份对 UMAP 嵌入数据进行着色来查看结果。

plt.scatter(standard_embedding[:, 0], standard_embedding[:, 1], c=kmeans_labels, s=0.1, cmap='Spectral');
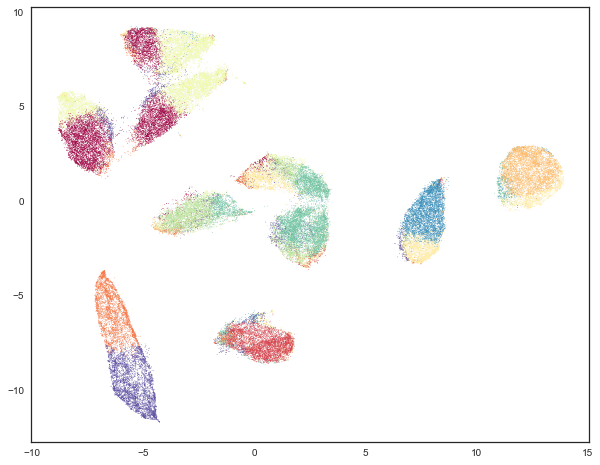
_images/clustering_10_1.png

这并不是我们真正想要的结果（尽管它确实揭示了 K-Means 如何在高维空间中选择簇以及 UMAP 如何通过寻找流形边界来展开流形的有趣特性）。虽然 K-Means 在某些情况下是正确的，例如右侧的两个簇大部分是正确的，但其余大部分数据看起来在剩余的簇之间被有些随意地分割了。我们可以通过评估此聚类与真实标签相比的调整兰德分数和调整互信息来验证这种印象。

(
    adjusted_rand_score(mnist.target, kmeans_labels),
    adjusted_mutual_info_score(mnist.target, kmeans_labels)
)

(0.36675295135972552, 0.49614118437750965)

正如预期的那样，我们做得并不特别好——两个分数都在 0 到 1 的范围内，其中 0 代表糟糕（基本随机）的聚类，而 1 代表完美恢复真实标签。K-Means 肯定不是随机的，但距离完美恢复真实标签也还有相当大的差距。部分问题在于 K-Means 的工作方式，它基于中心点，并假设簇大致呈球形——这是 K-Means 在数字类别之间产生一些明显分割的原因。我们可以通过使用更智能的基于密度的算法来潜在地改进这一点。在本例中，我们选择尝试 HDBSCAN，我们认为它是最先进的基于密度的技术之一。为了性能起见，我们将通过 PCA 将数据的维度降至 50 维（这恢复了大部分方差），因为 HDBSCAN 在处理高维数据时性能扩展性较差。

lowd_mnist = PCA(n_components=50).fit_transform(mnist.data)
hdbscan_labels = hdbscan.HDBSCAN(min_samples=10, min_cluster_size=500).fit_predict(lowd_mnist)

现在我们可以检查结果了。然而，在进行之前，应该注意的是 HDBSCAN 的一个特点是它可以拒绝对某些点进行聚类，并将它们分类为“噪声”。为了可视化这一方面，我们将被分类为噪声的点着色为灰色，然后根据簇成员身份对剩余的点着色。

clustered = (hdbscan_labels >= 0)
plt.scatter(standard_embedding[~clustered, 0],
            standard_embedding[~clustered, 1],
            color=(0.5, 0.5, 0.5),
            s=0.1,
            alpha=0.5)
plt.scatter(standard_embedding[clustered, 0],
            standard_embedding[clustered, 1],
            c=hdbscan_labels[clustered],
            s=0.1,
            cmap='Spectral');
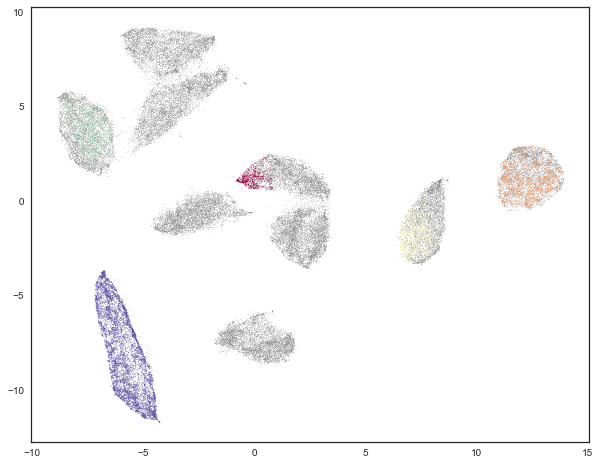
_images/clustering_16_1.png

这看起来有些差强人意。它通过简单地拒绝对大部分数据进行分类来实现 HDBSCAN“不错”的方法。结果是聚类几乎肯定无法恢复所有标签。我们可以通过查看聚类验证分数来验证这一点。

(
    adjusted_rand_score(mnist.target, hdbscan_labels),
    adjusted_mutual_info_score(mnist.target, hdbscan_labels)
)

(0.053830107882840102, 0.19756104096566332)

这些分数比 K-Means 差远了！部分原因是这些分数假定噪声点只是一个额外的簇。我们可以只查看 HDBSCAN 实际有足够信心分配到簇的数据子集——一个简单的子选择将允许我们仅对该数据重新计算分数。

clustered = (hdbscan_labels >= 0)
(
    adjusted_rand_score(mnist.target[clustered], hdbscan_labels[clustered]),
    adjusted_mutual_info_score(mnist.target[clustered], hdbscan_labels[clustered])
)

(0.99843407988303912, 0.99405521087764015)

在这里我们看到，在 HDBSCAN 愿意聚类的地方，它做得几乎完全正确。这就是它的设计目标——对其能做到的部分做到正确，而对其没有足够信心的部分则予以搁置。当然，这里的弊端在于它搁置了大量数据的聚类。HDBSCAN 实际上将多少数据分配到了簇中？我们可以很容易地计算出来。

np.sum(clustered) / mnist.data.shape[0]

0.17081428571428572

看起来只有不到 18% 的数据被聚类了。虽然 HDBSCAN 对它能聚类的数据做得很好，但在实际管理数据聚类方面做得却很差。这里的问题在于，作为一种基于密度的聚类算法，HDBSCAN 容易受到维度诅咒的影响：高维数据需要更多的观测样本才能产生足够的密度。如果我们能更多地降低数据的维度，密度就会变得更明显，HDBSCAN 聚类数据也会容易得多。问题在于，尝试使用 PCA 来做到这一点将会变得有问题。虽然降到 50 维仍然解释了数据的很多方差，但再进一步降低维度会迅速变得更糟。这是由于 PCA 的线性特性。我们需要的是强大的流形学习，而这正是 UMAP 可以发挥作用的地方。

UMAP 增强聚类

我们的目标是利用 UMAP 进行非线性流形感知降维，以便将数据集降至一个足够低的维度，使得基于密度的聚类算法能够取得进展。UMAP 在这方面的一个优势是它不要求你只降至两维——你可以降至 10 维，因为目标是聚类而不是可视化，而且 UMAP 的性能开销很小。碰巧 MNIST 是如此简单的数据集，我们可以一直降到只有两维，但一般来说，你应该探索不同的嵌入维度选项。

接下来需要注意的是，当使用 UMAP 进行降维时，您会希望选择与用于可视化时不同的参数。首先，我们会想要一个更大的 n_neighbors 值——较小的值会更关注非常局部的结构，并且更容易产生细粒度的簇结构，这可能更多是数据中噪声模式的结果，而非实际的簇。在本例中，我们将它从默认的 15 增加到 30。其次，将 min_dist 设置为一个非常低的值是有益的。因为我们实际上希望将点密集地聚集在一起（毕竟我们想要的是密度），所以一个低值会有所帮助，同时也会使簇之间的分离更清晰。在本例中，我们将简单地将 min_dist 设置为 0。

clusterable_embedding = umap.UMAP(
    n_neighbors=30,
    min_dist=0.0,
    n_components=2,
    random_state=42,
).fit_transform(mnist.data)

我们可以可视化其结果，看看它与更适合可视化参数相比如何

plt.scatter(clusterable_embedding[:, 0], clusterable_embedding[:, 1],
            c=mnist.target, s=0.1, cmap='Spectral');
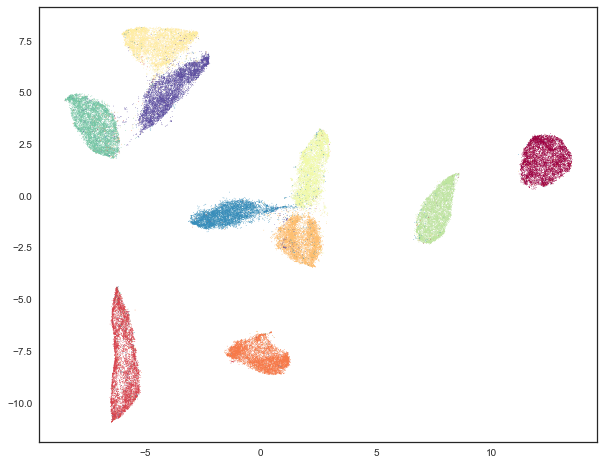
_images/clustering_27_1.png

如您所见，我们仍然保留了大致的全局结构，但我们将点更紧密地聚集在簇内，因此我们可以看到簇之间有更大的间隔。最终，这种嵌入仅用于聚类目的，从现在起，我们将回到原始嵌入进行可视化。

下一步是对这些数据进行聚类。我们将再次使用 HDBSCAN，参数设置与之前相同。

labels = hdbscan.HDBSCAN(
    min_samples=10,
    min_cluster_size=500,
).fit_predict(clusterable_embedding)

现在我们可以像之前一样可视化结果了。

clustered = (labels >= 0)
plt.scatter(standard_embedding[~clustered, 0],
            standard_embedding[~clustered, 1],
            color=(0.5, 0.5, 0.5),
            s=0.1,
            alpha=0.5)
plt.scatter(standard_embedding[clustered, 0],
            standard_embedding[clustered, 1],
            c=labels[clustered],
            s=0.1,
            cmap='Spectral');
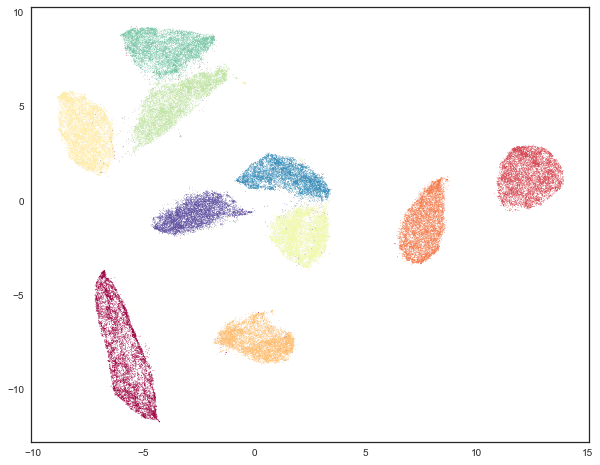
_images/clustering_31_1.png

我们可以看到，我们在寻找簇方面做得更好了，而不是仅仅将大部分数据归类为噪声。这是因为我们不再需要应对 50 维空间中相对缺乏密度的问题，现在 HDBSCAN 可以更清晰地辨别出簇。

我们还可以像之前一样使用聚类质量度量进行定量评估。

adjusted_rand_score(mnist.target, labels), adjusted_mutual_info_score(mnist.target, labels)

(0.9239306564265013, 0.90302671641133736)

之前 HDBSCAN 表现非常差，现在我们的分数达到 0.9 或更高。这是因为我们实际上聚类了更多的数据。和之前一样，我们还可以看看 HDBSCAN 只对那些它有信心聚类的数据表现如何。

clustered = (labels >= 0)
(
    adjusted_rand_score(mnist.target[clustered], labels[clustered]),
    adjusted_mutual_info_score(mnist.target[clustered], labels[clustered])
)

(0.93240371696811541, 0.91912906363537572)

这比原始的 HDBSCAN 差一点，但如果您做出更多预测，犯错的次数会更多，这并不令人意外。问题是 HDBSCAN 实际上聚类了多少数据？之前我们只聚类了 17% 的数据。

np.sum(clustered) / mnist.data.shape[0]

0.99164285714285716

现在我们聚类了超过 99% 的数据！而且我们在调整兰德分数和调整互信息方面的结果与使用卷积自编码器技术的当前最先进技术一致。对于一种仅仅将数据视为任意 784 维向量的方法来说，这已经很不错了。

希望这已经概述了 UMAP 对聚类的好处。正如所有事情一样，必须小心谨慎，但显然在明智使用的情况下，UMAP 可以提供明显更好的聚类结果。