UMAP 可复现性

UMAP 是一种随机算法——它利用随机性来加速近似步骤，并帮助解决困难的优化问题。这意味着 UMAP 的不同运行会产生不同的结果。UMAP 相对稳定——因此理想情况下不同运行之间的差异应该相对较小——但不同运行仍然可能存在变异。为了确保结果能够完全复现，UMAP 允许用户设置随机种子状态。

自 0.4 版本以来，UMAP 也支持多线程以提高性能；在执行优化时，这利用了线程之间的竞态条件在某些优化阶段是可以接受的事实。不幸的是，这意味着在多线程情况下 UMAP 输出的随机性不仅取决于输入的随机种子，还取决于优化期间线程之间的竞态条件，这是无法控制的。这意味着多线程 UMAP 的结果无法完全复现。

在本教程中，我们将探讨如何出于性能目的在多线程模式下使用 UMAP，以及如何通过固定随机状态来确保精确复现性，但这会牺牲一些性能。首先，让我们加载相关库并获取一些数据；在本例中是 MNIST 数字数据集。

import numpy as np
import sklearn.datasets
import umap
import umap.plot

data, labels = sklearn.datasets.fetch_openml(
    'mnist_784', version=1, return_X_y=True
)

准备好数据后，让我们对其运行 UMAP，并注意运行时间

%%time
mapper1 = umap.UMAP().fit(data)

CPU times: user 3min 18s, sys: 3.84 s, total: 3min 22s
Wall time: 1min 29s

这里需要注意的一点是，“实际时间”（Wall time）明显小于“CPU 时间”（CPU time）——这意味着使用了多个 CPU 核心。对于本次演示，我使用了最新版本的 PyNNDescent 进行最近邻搜索（如果安装了，UMAP 会使用它），它也支持多线程。结果是对数据进行了非常快速的拟合，有效利用了多个核心。如果您在一台拥有大量可用核心的大型服务器上，并且不希望使用 全部 核心（这是默认情况），您目前可以通过设置 numba 环境变量 NUMBA_NUM_THREADS 来控制使用的核心数量；更多详细信息请参阅 numba 文档。

现在让我们绘制结果，看看嵌入是什么样的

umap.plot.points(mapper1, labels=labels)
_images/reproducibility_6_1.png

现在，让我们再次运行 UMAP，并将结果与第一次运行的结果进行比较。

%%time
mapper2 = umap.UMAP().fit(data)

CPU times: user 2min 53s, sys: 4.16 s, total: 2min 57s
Wall time: 1min 5s

您会注意到这次运行 甚至更快。这是因为在第一次运行时，numba 仍在后台进行部分代码的 JIT（即时）编译。相比之下，这次这项工作已经完成，因此不再占用我们的运行时间。我们看到仍然很好地利用了多个核心。

现在让我们绘制第二次运行的结果并与第一次进行比较

umap.plot.points(mapper2, labels=labels)
_images/reproducibility_10_1.png

从定性上看，这看起来非常相似，但仔细检查会很快发现不同运行的结果实际上是不同的。请注意，即使在 0.4 版本之前的 UMAP 中也会出现这种情况——因为我们没有固定特定的随机种子，因此使用了系统当前的随机状态，而系统随机状态在不同运行之间自然会不同。这是默认行为，也是 sklearn 中随机估算器（estimators）的标准做法。用户需要显式提供随机种子，而不是拥有一个默认的随机种子，以便获得可复现的结果。正如 Vito Zanotelli 所指出的

... 设置随机种子就像签署一份放弃声明，表示“我清楚这是一个随机算法，并且我已经进行了充分的测试，以确认我的主要结论不受这种随机性的影响”。

考虑到这一点，让我们看看如果我们设置一个显式的 random_state 值会发生什么

%%time
mapper3 = umap.UMAP(random_state=42).fit(data)

CPU times: user 2min 27s, sys: 4.16 s, total: 2min 31s
Wall time: 1min 56s

首先要注意的是，这次运行花费的时间明显更长（尽管所有函数都已经通过 numba JIT 编译）。然后请注意，实际时间（Wall time）和 CPU 时间现在彼此更接近——我们不再在近似相同的程度上利用多个核心。这是因为通过设置 random_state，我们实际上关闭了任何不支持显式复现性的多线程。让我们绘制结果

umap.plot.points(mapper3, labels=labels)
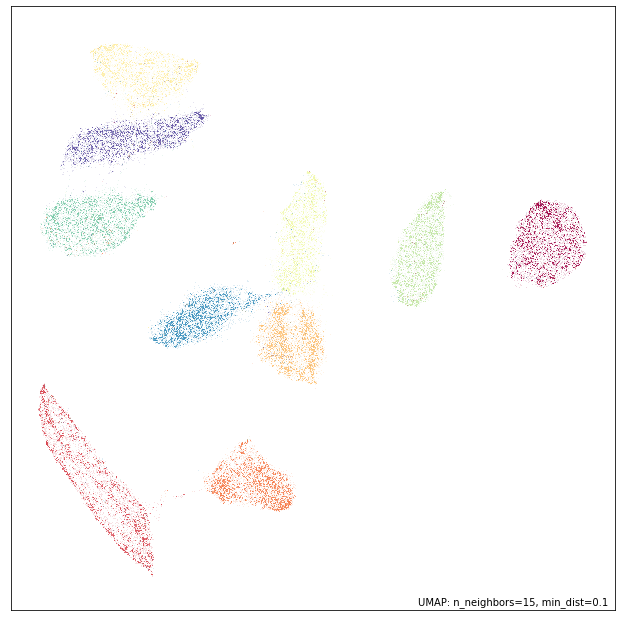
_images/reproducibility_14_1.png

从定性角度来看，我们得到了与之前非常相似的结果，但再次检查会发现存在一些差异。更重要的是，现在这个结果应该是可复现的。因此，我们可以使用相同的 random_state 设置再次运行 UMAP …

%%time
mapper4 = umap.UMAP(random_state=42).fit(data)

CPU times: user 2min 26s, sys: 4.13 s, total: 2min 30s
Wall time: 1min 54s

同样，这比之前未设置 random_state 的运行花费时间更长。然而，当我们绘制第二次运行的结果时，我们看到它们看起来不仅仅是定性相似，而是几乎完全相同

umap.plot.points(mapper4, labels=labels)
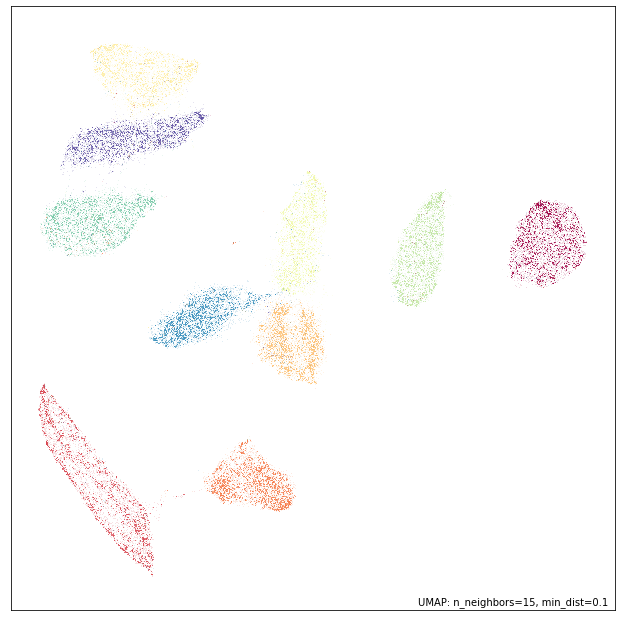
_images/reproducibility_18_1.png

事实上，我们可以通过验证结果嵌入的每一个坐标都完全匹配来检查结果是否完全相同

np.all(mapper3.embedding_ == mapper4.embedding_)

True

所以，我们实际上已经完全精确地复现了嵌入。