如何使用 AlignedUMAP

不同 UMAP 嵌入相互对齐有时可能很有益。有几种方法可以实现这一点。一种简单的方法是独立地使用 UMAP 嵌入每个数据集，然后在共享点上求解普罗克鲁斯特斯变换。另一种方法是嵌入第一个数据集，然后根据共享点在第一个嵌入中的位置为第二个数据集构建初始嵌入，然后从那里开始。第三种方法通常能提供更好的对齐，即在优化过程*中*同时优化两个嵌入，并对共享点在不同嵌入中占据不同位置的程度施加某种约束。最后一种方法是可行的，但自行实现并不容易（与前两种方法不同）。为了解决这个问题，umap-learn 中已将其实现为一个单独的模型类，名为 AlignedUMAP。这个类非常灵活，但在此我们将通过一些基本（且略显人为）的数据来演示其简单用法，仅为了展示如何让它在数据上运行。

import numpy as np
import sklearn.datasets
import umap
import umap.plot
import umap.utils as utils
import umap.aligned_umap
import matplotlib.pyplot as plt

为了演示，我们将仅使用 sklearn 中的 pendigits 数据集。

digits = sklearn.datasets.load_digits()

为了生成一系列数据集，其中每个不同数据集之间有一些共享点，我们将首先对数据进行排序，以便获得某种大致合理的进展。在这种情况下，我们将按手写数字中的“墨水”总量进行排序。这并不是说这样做有意义，而仅仅是为了提供一些有用的方法，可以将数据切分成重叠的块，我们希望分别嵌入这些块，同时保持对齐。

ordered_digits = digits.data[np.argsort(digits.data.sum(axis=1))]
ordered_target = digits.target[np.argsort(digits.data.sum(axis=1))]
plt.matshow(ordered_digits[-1].reshape((8,8)))

然后，我们可以将数据集分成每份 400 个样本的切片，以 150 个样本为一块向前移动，以确保连续切片之间存在重叠。这将为我们提供一个包含十个不同数据集的列表，我们可以对其进行嵌入，目标是确保点在嵌入中的位置相对一致。

slices = [ordered_digits[150 * i:min(ordered_digits.shape[0], 150 * i + 400)] for i in range(10)]

为了确保一致性，AlignedUMAP 将需要比 *仅* 数据集更多信息——我们还需要一些关于数据集之间如何关联的信息。这些信息以字典的形式存在，用于关联一个数据集的索引与另一个数据集的索引。目前，AlignedUMAP 仅支持序列化数据集，并在序列中每个连续对之间建立关系。为了构建此数据集的关系，我们注意到一个数据集的最后 250 个样本与下一个数据集的前 250 个样本是相同的样本——这使得构建字典变得容易：它映射的是

150 --> 0
151 --> 1
...
398 --> 248
399 --> 249

我们可以使用字典推导轻松构建它。每个连续对之间将具有相同的关系，因此要创建对之间的关系列表，我们只需将构建好的关系复制所需的次数即可。

relation_dict = {i+150:i for i in range(400-150)}
relation_dicts = [relation_dict.copy() for i in range(len(slices) - 1)]

请注意，虽然在此示例中，关系定义了不同数据集中相同样本之间的映射，但它可能更加通用——请参阅后面的政治示例，其中关系是根据外部信息（代表的姓名和州）构建的。

现在我们既有了数据切片列表，又有了连续对之间的关系列表，我们可以使用 AlignedUMAP 类生成一个嵌入列表。AlignedUMAP 类接受 UMAP 的大部分参数。主要区别在于 fit 方法需要一个数据集的 *列表*，以及一个指定连续数据集对之间关系字典的关键字参数 relations。除此之外，其他操作基本上是一键式的。

%%time
aligned_mapper = umap.AlignedUMAP().fit(slices, relations=relation_dicts)

CPU times: user 57.4 s, sys: 8.43 s, total: 1min 5s
Wall time: 57.4 s

您会注意到，尽管使用了相对较小的 pendigits 数据集，但这花了不少时间运行。这是因为我们一次完成了 10 个不同的 UMAP 嵌入，因此平均每个嵌入大约需要五秒钟，这更合理——然而，对齐确实会产生额外的开销。

下一步是查看结果。为了确保生成的图具有一致的 x 轴和 y 轴，我们将使用一个小型函数来计算绘图的坐标轴边界。

def axis_bounds(embedding):
    left, right = embedding.T[0].min(), embedding.T[0].max()
    bottom, top = embedding.T[1].min(), embedding.T[1].max()
    adj_h, adj_v = (right - left) * 0.1, (top - bottom) * 0.1
    return [left - adj_h, right + adj_h, bottom - adj_v, top + adj_v]

现在只需将结果绘制在十个不同的散点图中即可。我们可以直接使用 matplotlib 最轻松地做到这一点，设置一个图网格。请注意，进展是按行然后按列进行的，所以请按照阅读文本页的方式（先横后竖）阅读进展。

fig, axs = plt.subplots(5,2, figsize=(10, 20))
ax_bound = axis_bounds(np.vstack(aligned_mapper.embeddings_))
for i, ax in enumerate(axs.flatten()):
    current_target = ordered_target[150 * i:min(ordered_target.shape[0], 150 * i + 400)]
    ax.scatter(*aligned_mapper.embeddings_[i].T, s=2, c=current_target, cmap="Spectral")
    ax.axis(ax_bound)
    ax.set(xticks=[], yticks=[])
plt.tight_layout()

因此，尽管是不同数据集上的不同嵌入，聚类仍保持其整体对齐——左上角图和右下角图对于特定数字聚类具有大致相同的位置。我们也可以在一定程度上看到结构如何随着不同切片的变化而改变。因此，我们保持了各种嵌入的对齐，但允许由每个不同数据切片的不同结构所决定的变化。

在线更新对齐嵌入

我们可能有流入的时间数据，并希望时间窗口的嵌入能够（理想情况下）与先前时间窗口的嵌入对齐。只要我们使用的时间窗口重叠以允许时间窗口之间建立关系，这是可能的——除了之前的代码需要将所有时间窗口 *一次性* 输入才能进行拟合。我们反而希望训练一个初始模型，然后随着数据的到来进行更新。这可以通过 update 方法实现，我们将在下面进行演示。

首先我们需要拟合一个基础 AlignedUMAP 模型；我们将使用前两个切片和第一个关系字典来实现。

%%time
updating_mapper = umap.AlignedUMAP().fit(slices[:2], relations=relation_dicts[:1])

CPU times: user 9.32 s, sys: 1.47 s, total: 10.8 s
Wall time: 9.17 s

请注意，这相当快，因为我们只拟合了两个切片。给定训练好的模型，update 方法需要添加一个新的数据切片，以及一个关系字典（像使用 fit 一样通过 relations 关键字参数传入）。这将为新数据在模型的 embeddings_ 属性中附加一个新的嵌入，并与目前为止看到的内容对齐。

for i in range(2,len(slices)):
    %time updating_mapper.update(slices[i], relations={v:k for k,v in relation_dicts[i-1].items()})

CPU times: user 7.78 s, sys: 1.15 s, total: 8.93 s
Wall time: 7.92 s
CPU times: user 6.64 s, sys: 1.17 s, total: 7.81 s
Wall time: 6.6 s
CPU times: user 6.94 s, sys: 1.17 s, total: 8.11 s
Wall time: 6.81 s
CPU times: user 6.45 s, sys: 1.51 s, total: 7.96 s
Wall time: 6.45 s
CPU times: user 7.44 s, sys: 1.32 s, total: 8.76 s
Wall time: 7.16 s
CPU times: user 7.68 s, sys: 1.73 s, total: 9.41 s
Wall time: 7.59 s
CPU times: user 7.88 s, sys: 1.65 s, total: 9.54 s
Wall time: 7.39 s
CPU times: user 7.82 s, sys: 1.98 s, total: 9.8 s
Wall time: 7.7 s

请注意，每个新的切片所需时间相对较短，正如我们所希望的那样。这方面的缺点是，正如您可以想象的，我们没有“向前”关系——切片上的窗口只向后看。这意味着结果不太理想，但我们牺牲了这一点换取了随数据到来快速轻松更新的能力。

我们可以使用与之前基本相同的代码来查看结果。

fig, axs = plt.subplots(5,2, figsize=(10, 20))
ax_bound = axis_bounds(np.vstack(updating_mapper.embeddings_))
for i, ax in enumerate(axs.flatten()):
    current_target = ordered_target[150 * i:min(ordered_target.shape[0], 150 * i + 400)]
    ax.scatter(*updating_mapper.embeddings_[i].T, s=2, c=current_target, cmap="Spectral")
    ax.axis(ax_bound)
    ax.set(xticks=[], yticks=[])
plt.tight_layout()

我们可以看到对齐确实奏效了，因此新的切片与先前训练的切片保持可比性。正如所指出的那样，整体对齐和进展不如之前的版本好，但它确实具有允许随数据到来进行更新的重要优势。

请注意，目前这个模型保留了所有之前的数据，因此它实际上只适用于批量流式方法，即偶尔训练一个新模型，在继续更新之前丢弃一部分历史数据。

对齐不同参数

可以对齐使用不同参数而不是不同数据的 UMAP 嵌入。为了演示这是如何工作的，我们将继续使用 pendigits 数据集，但我们不切割数据，而是使用完整数据集。这意味着数据集之间的关系是简单的恒定关系。我们可以提前构建这些关系

constant_dict = {i:i for i in range(digits.data.shape[0])}
constant_relations = [constant_dict for i in range(9)]

要在参数范围内运行 AlignedUMAP，您只需传入一个您希望使用的参数序列的 *列表*。您可以为几个不同的参数执行此操作——只需确保所有列表长度相同！在这种情况下，我们将尝试查看如果更改 n_neighbors 和 min_dist，嵌入会如何变化。这意味着当我们创建 AlignedUMAP 对象时，我们为每个参数传递一个列表，而不是单个值。为了使可视化稍微更有趣一些，我们还将更改一些对齐参数（只有两个主要参数）。具体来说，我们将调整 alignment_window_size，它控制在进行对齐时我们在数据集上向前和向后查看的范围，以及 alignment_regularisation，它控制我们对对齐方面与 UMAP 布局方面的权重。较大的 alignment_regularisation 值会更努力地保持点在不同嵌入之间对齐（代价是每个切片的嵌入质量），而较小的值将允许优化更多地关注单个嵌入，并减少对齐嵌入的强调。

有了模型后，我们就可以进行拟合了。和之前一样，我们需要向它提供一个数据集列表和一个关系列表。由于我们每次都使用相同的数据（并改变参数），我们只需重复完整的 pendigits 数据集即可。请注意，数据集的数量需要与使用的参数值的数量匹配。关系的數量（比参数值的数量少一个）也是如此。

neighbors_mapper = umap.AlignedUMAP(
    n_neighbors=[3,4,5,7,11,16,22,29,37,45,54],
    min_dist=[0.01,0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45],
    alignment_window_size=2,
    alignment_regularisation=1e-3,
).fit(
    [digits.data for i in range(10)], relations=constant_relations
)

和以前一样，我们可以通过绘制每个嵌入来查看结果。

fig, axs = plt.subplots(5,2, figsize=(10, 20))
ax_bound = axis_bounds(np.vstack(neighbors_mapper.embeddings_))
for i, ax in enumerate(axs.flatten()):
    ax.scatter(*neighbors_mapper.embeddings_[i].T, s=2, c=digits.target, cmap="Spectral")
    ax.axis(ax_bound)
    ax.set(xticks=[], yticks=[])
plt.tight_layout()

为了更好地了解嵌入随着参数值变化而演变的感受，我们可以将数据绘制在三维空间中，其中第三维是选择的参数值。为了更好地展示嵌入中的数据点如何随着参数变化而 *移动*，我们可以不将它们绘制成点，而是绘制成连接每个连续嵌入中相同点的 *曲线*。对于这样的三维图，我们将使用 plotly 绘图库。

import plotly.graph_objects as go
import plotly.express as px
import pandas as pd

我们首先要做的是将数据整理成适合 plotly 的格式。这也是我们加载 pandas 的原因——plotly 喜欢数据框。这包括将所有嵌入堆叠在一起，然后根据我们所在的嵌入分配一个额外的 z 值。为了可视化的目的，我们只需要一个从 0 到 1 的线性刻度，长度适合 z 坐标。

n_embeddings = len(neighbors_mapper.embeddings_)
es = neighbors_mapper.embeddings_
embedding_df = pd.DataFrame(np.vstack(es), columns=('x', 'y'))
embedding_df['z'] = np.repeat(np.linspace(0, 1.0, n_embeddings), es[0].shape[0])
embedding_df['id'] = np.tile(np.arange(es[0].shape[0]), n_embeddings)
embedding_df['digit'] = np.tile(digits.target, n_embeddings)

我们可以做的下一件事是平滑曲线，而不是让它们保持分段线性。为此，我们可以使用 scipy.interpolate 功能创建通过我们希望创建的曲线上所有点的平滑三次样条。

import scipy.interpolate

插值模块有一个函数 interp1d，它根据需要通过的一维数据点集生成一个（向量的）平滑函数。我们可以为每个 pendigit 样本的 x 和 y 坐标生成单独的函数，从而生成三维平滑曲线。

fx = scipy.interpolate.interp1d(
    embedding_df.z[embedding_df.id == 0], embedding_df.x.values.reshape(n_embeddings, digits.data.shape[0]).T, kind="cubic"
)
fy = scipy.interpolate.interp1d(
    embedding_df.z[embedding_df.id == 0], embedding_df.y.values.reshape(n_embeddings, digits.data.shape[0]).T, kind="cubic"
)
z = np.linspace(0, 1.0, 100)

有了这些准备，只需绘制所有曲线即可。在 plotly 的说法中，每条曲线都是一个“trace”，我们分别生成每条曲线（以及由样本代表的数字给出的合适颜色）。然后我们将所有 trace 添加到图中，并显示图。

palette = px.colors.diverging.Spectral
interpolated_traces = [fx(z), fy(z)]
traces = [
    go.Scatter3d(
        x=interpolated_traces[0][i],
        y=interpolated_traces[1][i],
        z=z*3.0,
        mode="lines",
        line=dict(
            color=palette[digits.target[i]],
            width=3.0
        ),
        opacity=1.0,
    )
    for i in range(digits.data.shape[0])
]
fig = go.Figure(data=traces)
fig.update_layout(
    width=800,
    height=700,
    autosize=False,
    showlegend=False,
)
fig.show()

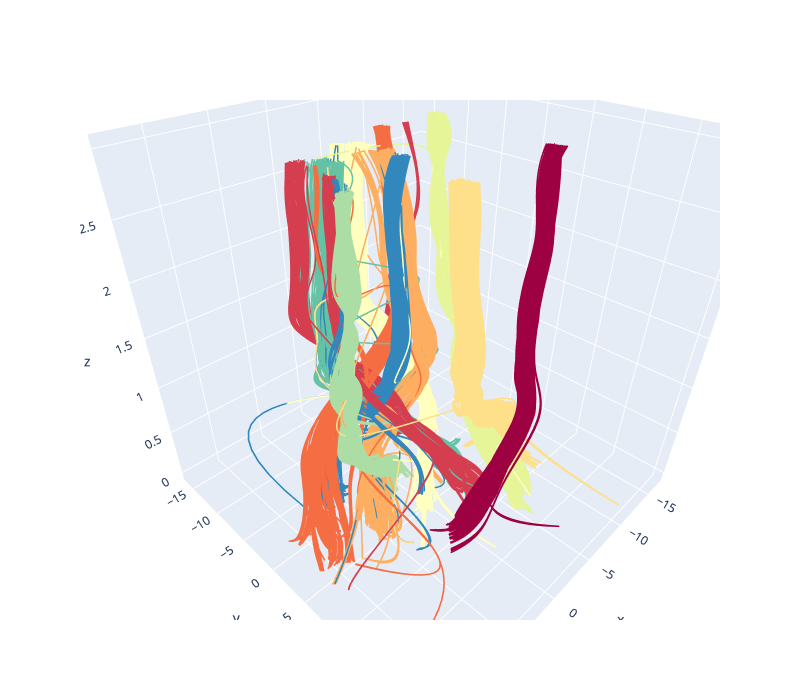
由于将交互式 plotly 图嵌入文档中很棘手，这里提供了一张静态图片，但如果您自己运行此代码，您将看到数据的完全交互式视图。

或者，我们可以通过将每个 z 切片渲染为动画 GIF 中的一帧，将第三维可视化为嵌入随时间推移的演变。为此，我们首先需要导入一些 notebook 显示工具和 matplotlib 的 animation 模块。

from IPython.display import display, Image, HTML
from matplotlib import animation

接下来，我们将创建一个新图，初始化一个空白散点图，然后使用 FuncAnimation 逐帧更新点位置（称为“offsets”）。

fig = plt.figure(figsize=(4, 4), dpi=150)
ax = fig.add_subplot(1, 1, 1)

scat = ax.scatter([], [], s=2)
scat.set_array(digits.target)
scat.set_cmap('Spectral')
text = ax.text(ax_bound[0] + 0.5, ax_bound[2] + 0.5, '')
ax.axis(ax_bound)
ax.set(xticks=[], yticks=[])
plt.tight_layout()

offsets = np.array(interpolated_traces).T
num_frames = offsets.shape[0]

def animate(i):
    scat.set_offsets(offsets[i])
    text.set_text(f'Frame {i}')
    return scat

anim = animation.FuncAnimation(
    fig,
    init_func=None,
    func=animate,
    frames=num_frames,
    interval=40)

然后我们可以将动画保存为 GIF 并关闭动画。根据您的机器，您可能需要更改 save 方法使用的写入器。

anim.save("aligned_umap_pendigits_anim.gif", writer="pillow")
plt.close(anim._fig)

最后，我们可以读取渲染的 GIF 并在 notebook 中显示它。

with open("aligned_umap_pendigits_anim.gif", "rb") as f:
    display(Image(f.read()))