逆变换

UMAP 提供对逆变换的支持——给定低维嵌入空间中的位置，生成高维数据样本。首先，让我们加载所有相关的库。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
import seaborn as sns
import sklearn.datasets
import umap
import umap.plot

我们需要一些数据进行测试。首先，我们将使用 MNIST 数字数据集。这是一个包含 70000 个手写数字的数据集，编码为 28x28 像素的灰度图像。我们的目标是使用 UMAP 将该数据集的维度降低到较小的程度，然后看看是否可以通过从嵌入空间中采样点来生成新的数字。要加载 MNIST 数据集，我们将使用 sklearn 的 fetch_openml 函数。

data, labels = sklearn.datasets.fetch_openml('mnist_784', version=1, return_X_y=True)

现在我们需要生成这些数据的降维表示。使用 UMAP 实现这一点很直接，但在本例中，我们不使用 fit_transform，而是使用 fit 方法，以便保留训练好的模型，以便后续根据嵌入空间的样本生成新的数字。

mapper = umap.UMAP(random_state=42).fit(data)

为了确保一切正常，我们可以绘制数据（因为我们已将其降至二维）。我们将使用 umap.plot 功能来完成此操作。

umap.plot.points(mapper, labels=labels)
_images/inverse_transform_7_1.png

结果看起来与我们预期的一致。不同的数字类别已得到不错的区分。现在，我们需要在嵌入空间中创建一组样本，以便对其应用 inverse_transform 操作。为此，我们将生成一个样本网格，在四个角点之间进行线性插值。为了使我们的选择更有趣，我们将仔细选择跨越数据集的角点，并采样不同的数字，以便更好地观察过渡效果。

corners = np.array([
    [-5, -10],  # 1
    [-7, 6],  # 7
    [2, -8],  # 2
    [12, 4],  # 0
])

test_pts = np.array([
    (corners[0]*(1-x) + corners[1]*x)*(1-y) +
    (corners[2]*(1-x) + corners[3]*x)*y
    for y in np.linspace(0, 1, 10)
    for x in np.linspace(0, 1, 10)
])

现在我们可以将 inverse_transform 方法应用于这组测试点。每个测试点是位于嵌入空间中某个位置的二维点。inverse_transform 方法会将其转换为在这种位置上本应嵌入的高维表示的近似值。遵循 sklearn API，这就像调用训练模型的 inverse_transform 方法并将我们想要转换成高维表示的测试点集传递给它一样简单易用。请注意，这在计算上可能相当昂贵。

inv_transformed_points = mapper.inverse_transform(test_pts)

现在目标是可视化我们做得如何。实际上，我们希望做的是在嵌入空间中显示测试点，然后显示由逆变换生成的对应图像网格。将所有这些放在一个 matplotlib 图形中需要一些设置，但这相当容易管理——主要只是管理 GridSpec 格式。完成设置后，我们只需要一个嵌入的散点图、一个测试点的散点图，最后是一个我们生成的图像网格（将逆变换后的向量转换回图像只需将其重塑回 28x28 像素网格并使用 imshow）。

# Set up the grid
fig = plt.figure(figsize=(12,6))
gs = GridSpec(10, 20, fig)
scatter_ax = fig.add_subplot(gs[:, :10])
digit_axes = np.zeros((10, 10), dtype=object)
for i in range(10):
    for j in range(10):
        digit_axes[i, j] = fig.add_subplot(gs[i, 10 + j])

# Use umap.plot to plot to the major axis
# umap.plot.points(mapper, labels=labels, ax=scatter_ax)
scatter_ax.scatter(mapper.embedding_[:, 0], mapper.embedding_[:, 1],
                   c=labels.astype(np.int32), cmap='Spectral', s=0.1)
scatter_ax.set(xticks=[], yticks=[])

# Plot the locations of the text points
scatter_ax.scatter(test_pts[:, 0], test_pts[:, 1], marker='x', c='k', s=15)

# Plot each of the generated digit images
for i in range(10):
    for j in range(10):
        digit_axes[i, j].imshow(inv_transformed_points[i*10 + j].reshape(28, 28))
        digit_axes[i, j].set(xticks=[], yticks=[])
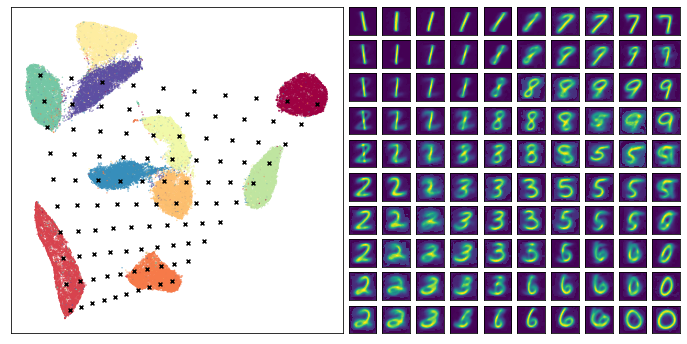
_images/inverse_transform_13_0.png

最终结果看起来相当不错——我们确实生成了看起来合理的数字图像，并且许多过渡（例如顶行从 1 到 7 的过渡）看起来非常自然且合理。这可以帮助您理解数字 1 集群的结构（它在角度上过渡，倾向于最终会变成 7 的方向），以及为什么 7 和 9 在嵌入中彼此靠近。当然，也有一些奇怪的过渡，特别是当测试点落入嵌入中集群之间的较大空白区域时——从某种意义上说，很难解释这些空白区域应该代表什么，因为它们并不真正代表平滑的过渡)。

进一步注意：所选择的测试点都没有落在嵌入的凸包之外。这是故意的——逆变换函数在该凸包边界之外效果不佳。请注意，如果您选择在嵌入边界之外的点进行逆变换，很可能会得到奇怪的结果（通常只是简单地捕捉到某个特定的源高维向量）。

让我们通过查看 Fashion MNIST 数据集继续演示。和之前一样，我们可以通过 sklearn 加载它。

data, labels = sklearn.datasets.fetch_openml('Fashion-MNIST', version=1, return_X_y=True)

同样，我们可以使用 UMAP 对这些数据进行拟合并获得一个映射器对象。

mapper = umap.UMAP(random_state=42).fit(data)

让我们绘制嵌入结果，看看我们得到了什么。

umap.plot.points(mapper, labels=labels)
_images/inverse_transform_20_1.png

同样，我们将通过在四个角点之间进行网格插值来生成一组测试点。和之前一样，我们将选择角点，以便我们能保持在嵌入点的凸包内，并确保逆变换不会发生太奇怪的事情。

corners = np.array([
    [-2, -6],  # bags
    [-9, 3],  # boots?
    [7, -5],  # shirts/tops/dresses
    [4, 10],  # pants
])

test_pts = np.array([
    (corners[0]*(1-x) + corners[1]*x)*(1-y) +
    (corners[2]*(1-x) + corners[3]*x)*y
    for y in np.linspace(0, 1, 10)
    for x in np.linspace(0, 1, 10)
])

现在我们像之前一样简单地应用逆变换。再次警告，这在计算上相当昂贵，可能需要一些时间才能完成。

inv_transformed_points = mapper.inverse_transform(test_pts)

现在我们可以使用与上面类似的代码来设置我们的嵌入图，叠加测试点和生成的图像。

# Set up the grid
fig = plt.figure(figsize=(12,6))
gs = GridSpec(10, 20, fig)
scatter_ax = fig.add_subplot(gs[:, :10])
digit_axes = np.zeros((10, 10), dtype=object)
for i in range(10):
    for j in range(10):
        digit_axes[i, j] = fig.add_subplot(gs[i, 10 + j])

# Use umap.plot to plot to the major axis
# umap.plot.points(mapper, labels=labels, ax=scatter_ax)
scatter_ax.scatter(mapper.embedding_[:, 0], mapper.embedding_[:, 1],
                   c=labels.astype(np.int32), cmap='Spectral', s=0.1)
scatter_ax.set(xticks=[], yticks=[])

# Plot the locations of the text points
scatter_ax.scatter(test_pts[:, 0], test_pts[:, 1], marker='x', c='k', s=15)

# Plot each of the generated digit images
for i in range(10):
    for j in range(10):
        digit_axes[i, j].imshow(inv_transformed_points[i*10 + j].reshape(28, 28))
        digit_axes[i, j].set(xticks=[], yticks=[])
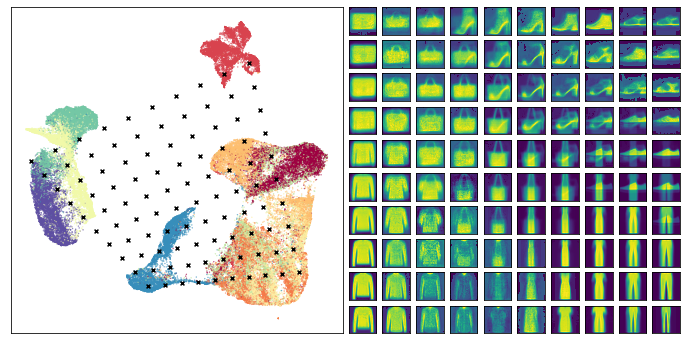
_images/inverse_transform_26_0.png

这次我们看到一些物品之间的插值看起来相当奇怪——特别是位于鞋子和裤子之间的点——最终，它在处理一个难题时已经尽力了。与此同时，许多其他的过渡似乎效果不错，因此它确实提供了关于嵌入结构的有益信息。