UMAP 基本参数
UMAP 是一种相当灵活的非线性降维算法。它试图学习数据的流形结构,并找到一个保留该流形基本拓扑结构的低维嵌入。在本 Notebook 中,我们将生成一些可可视化的 4 维数据,演示如何使用 UMAP 提供其 2 维表示,然后探讨各种 UMAP 参数如何影响最终的嵌入。本文档基于 Philippe Rivière 为 visionscarto.net 所做的工作。
首先,我们需要一些基本库。首先,需要使用numpy进行基本的数组操作。由于我们将可视化结果,因此需要matplotlib和seaborn。最后,我们需要umap本身来进行降维。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
import umap
%matplotlib inline
sns.set(style='white', context='poster', rc={'figure.figsize':(14,10)})
接下来,我们需要一些数据来嵌入到较低维度的表示中。为了使 4 维数据“可视化”,我们将从一个 4 维立方体中均匀随机生成数据,以便我们可以将样本解释为指定颜色(和透明度)的 (R,G,B,a) 值元组。因此,当我们绘制低维表示时,每个点都可以根据其 4 维值着色。为此,我们可以使用numpy。为了保持一致性,我们将固定随机种子。
np.random.seed(42)
data = np.random.rand(800, 4)
现在我们需要找到数据的低维表示。如基本用法文档所述,我们可以通过在UMAP对象上使用fit_transform()方法来完成。
fit = umap.UMAP()
%time u = fit.fit_transform(data)
CPU times: user 7.73 s, sys: 211 ms, total: 7.94 s
Wall time: 6.8 s
生成的值u是数据的 2 维表示。我们可以使用matplotlib绘制u的散点图来可视化结果。我们可以根据原始数据中关联的 4 维颜色为散点图中的每个点着色。
plt.scatter(u[:,0], u[:,1], c=data)
plt.title('UMAP embedding of random colours');
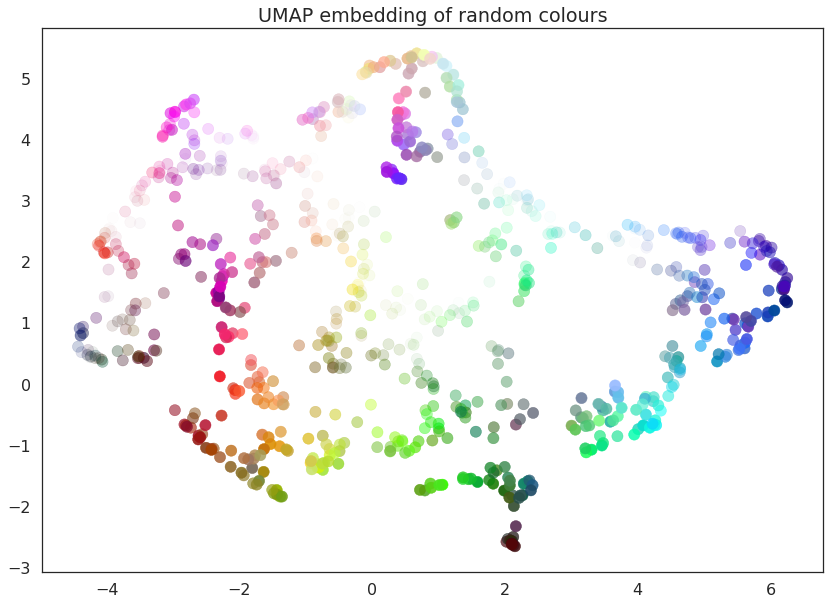
正如您所见,结果是数据被放置在 2 维空间中,使得在 4 维空间中附近(即颜色相似)的点保持靠近。由于我们在颜色立方体中随机选取了点,因此随机点在颜色空间中聚集的位置会产生一定的诱导结构。
UMAP 有几个超参数,它们对最终的嵌入结果有显著影响。在本 Notebook 中,我们将介绍四个主要的参数
n_neighborsmin_distn_componentsmetric
这些参数中的每一个都有不同的效果,我们将依次查看它们。为了简化探索,我们将首先编写一个简单的实用函数,该函数可以根据一组参数选择使用 UMAP 拟合数据,并绘制结果。
def draw_umap(n_neighbors=15, min_dist=0.1, n_components=2, metric='euclidean', title=''):
fit = umap.UMAP(
n_neighbors=n_neighbors,
min_dist=min_dist,
n_components=n_components,
metric=metric
)
u = fit.fit_transform(data);
fig = plt.figure()
if n_components == 1:
ax = fig.add_subplot(111)
ax.scatter(u[:,0], range(len(u)), c=data)
if n_components == 2:
ax = fig.add_subplot(111)
ax.scatter(u[:,0], u[:,1], c=data)
if n_components == 3:
ax = fig.add_subplot(111, projection='3d')
ax.scatter(u[:,0], u[:,1], u[:,2], c=data, s=100)
plt.title(title, fontsize=18)
n_neighbors
此参数控制 UMAP 如何平衡数据的局部结构和全局结构。它通过限制 UMAP 在尝试学习数据流形结构时考虑的局部邻域的大小来实现这一点。这意味着n_neighbors的低值将迫使 UMAP 专注于非常局部的结构(可能不利于全局视图),而高值将促使 UMAP 在估计数据流形结构时查看每个点的较大邻域,为了获得更广泛的数据视图而牺牲精细的细节结构。
我们可以通过使用 UMAP 拟合一系列n_neighbors值来在实践中看到这一点。UMAP 的n_neighbors默认值(如上所述)是 15,但我们将查看从 2(流形的非常局部视图)到 200(数据的四分之一)范围内的值。
for n in (2, 5, 10, 20, 50, 100, 200):
draw_umap(n_neighbors=n, title='n_neighbors = {}'.format(n))
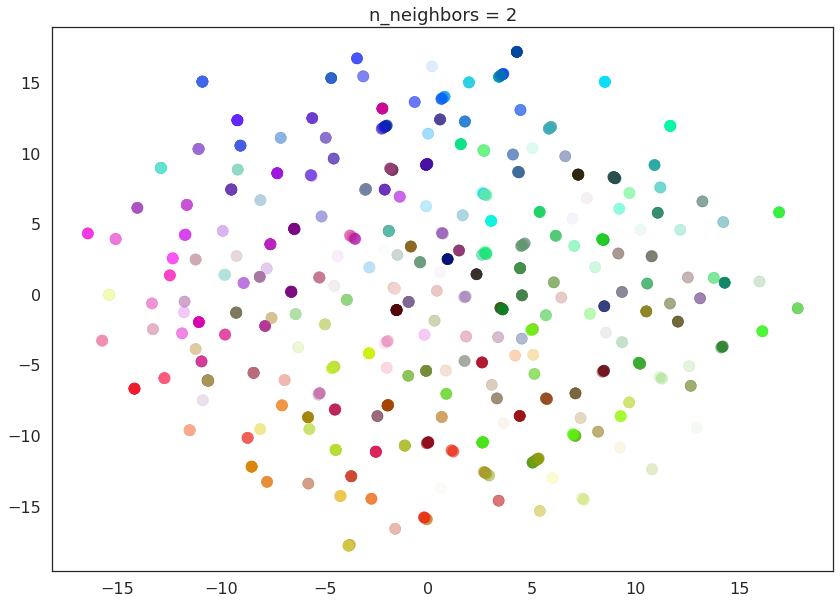
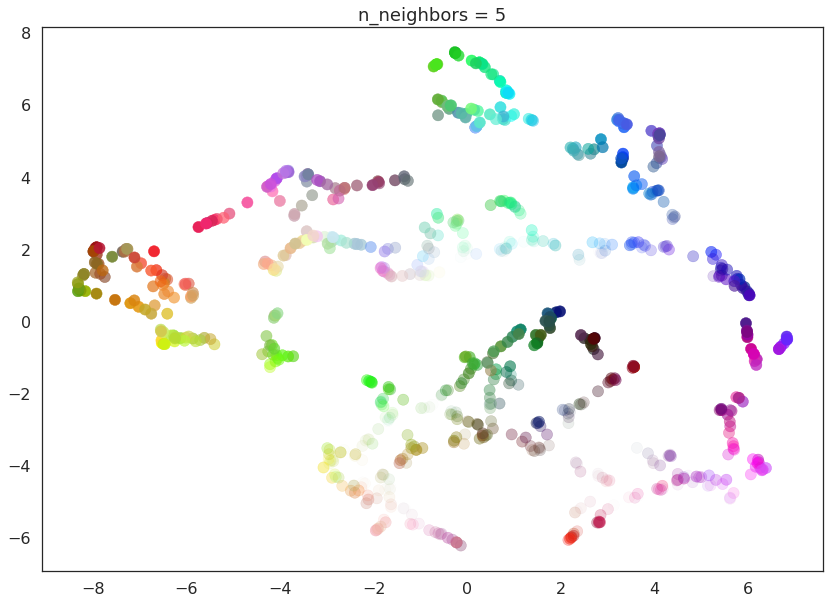
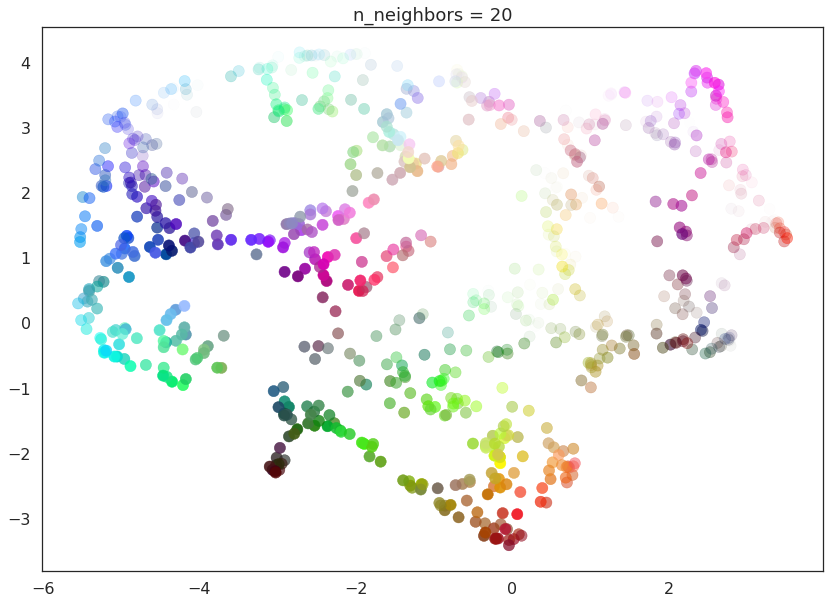
当n_neighbors=2时,我们看到 UMAP 只是将小链条粘合在一起,但由于视图狭窄/局部,无法看到它们如何连接。它还留下了许多不同的组件(甚至独立的点)。这表示从精细细节的角度来看,数据非常断开且分散在空间中。
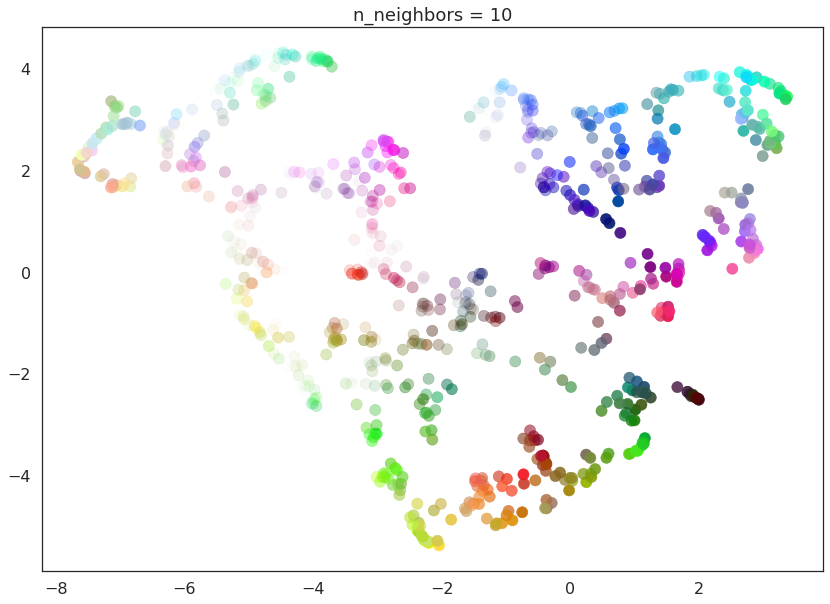
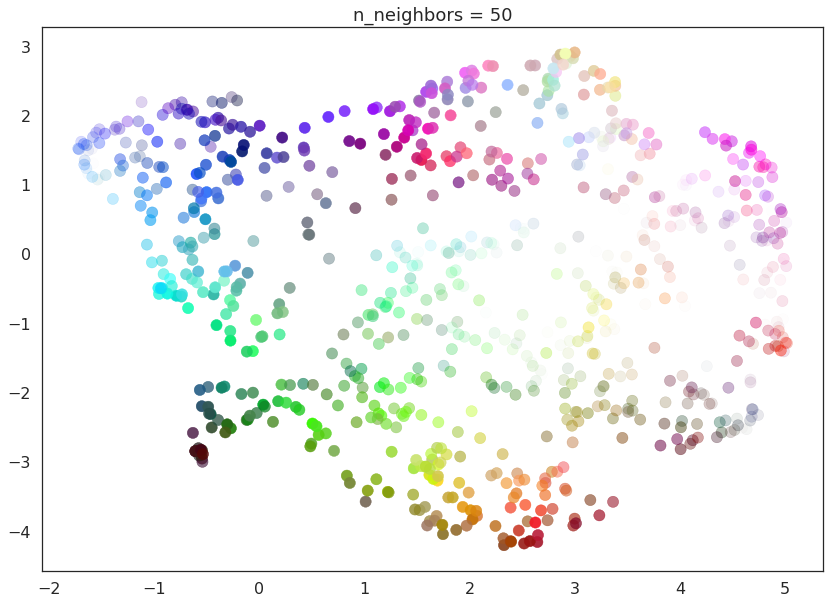
随着n_neighbors的增加,UMAP 能够看到更多数据的整体结构,将更多组件粘合在一起,并更好地覆盖数据的更广泛结构。到n_neighbors=20时,我们已经对数据有了相当好的整体视图,展示了整个数据集中各种颜色如何相互关联。
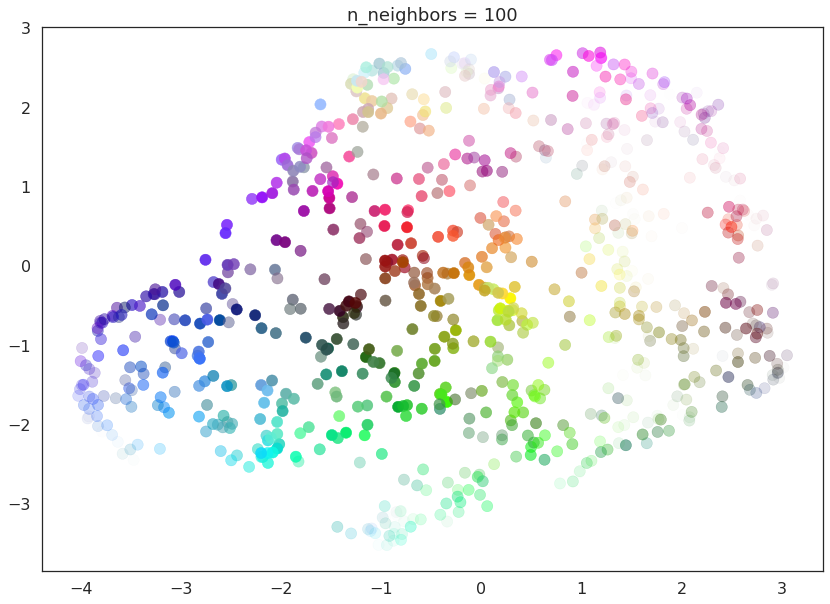
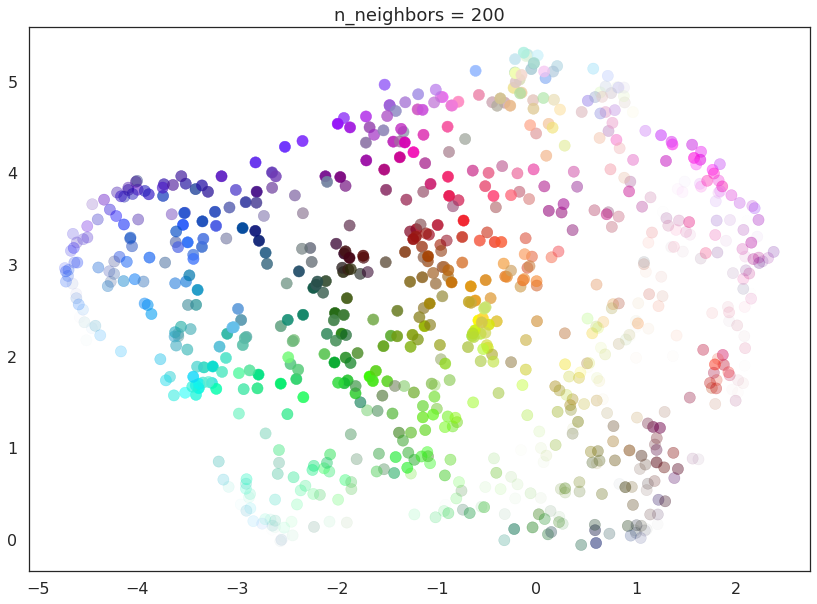
随着n_neighbors进一步增加,数据的整体结构越来越受到关注。这导致当n_neighbors=200时,整体结构(蓝色、绿色和红色;高亮度对比低亮度)得到了很好的捕捉,但牺牲了一些更精细的局部结构(单个颜色不再一定紧挨着它们最接近的颜色匹配)。
这种效果很好地体现了n_neighbors提供的局部/全局权衡。
min_dist
min_dist参数控制 UMAP 允许将点打包在一起的紧密程度。它字面上提供了点在低维表示中允许保持的最小距离。这意味着min_dist的低值将导致嵌入更加密集。如果您对聚类或更精细的拓扑结构感兴趣,这会很有用。min_dist的较大值将阻止 UMAP 将点打包在一起,而是专注于保留广泛的拓扑结构。
min_dist的默认值(如上所述)是 0.1。我们将查看从 0.0 到 0.99 范围内的值。
for d in (0.0, 0.1, 0.25, 0.5, 0.8, 0.99):
draw_umap(min_dist=d, title='min_dist = {}'.format(d))
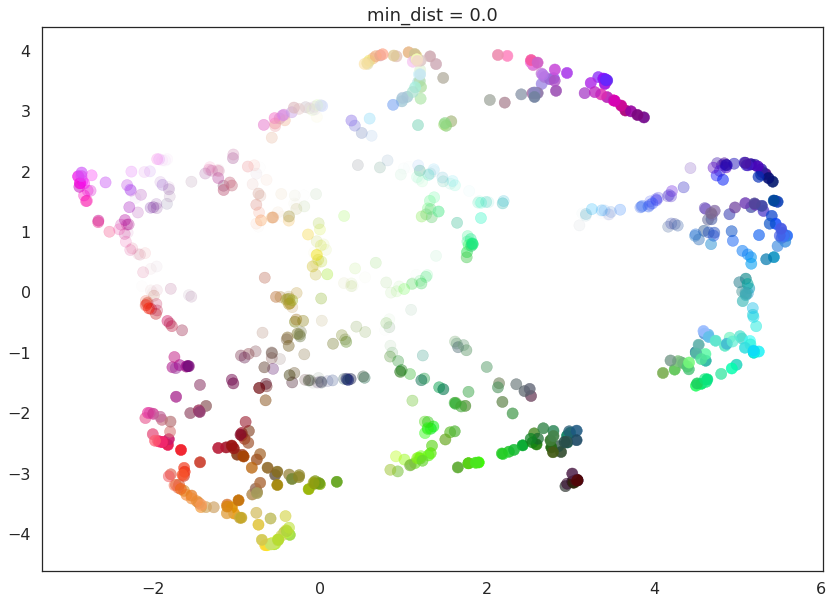
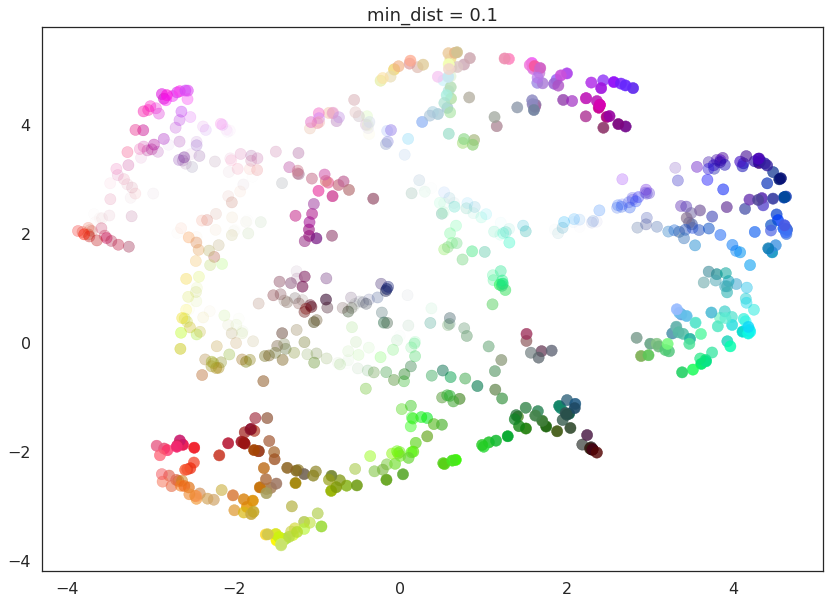
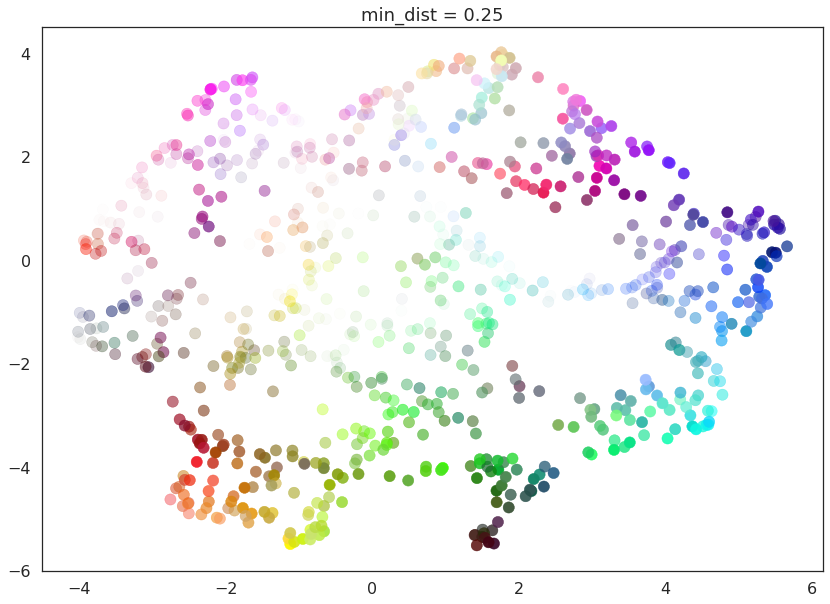
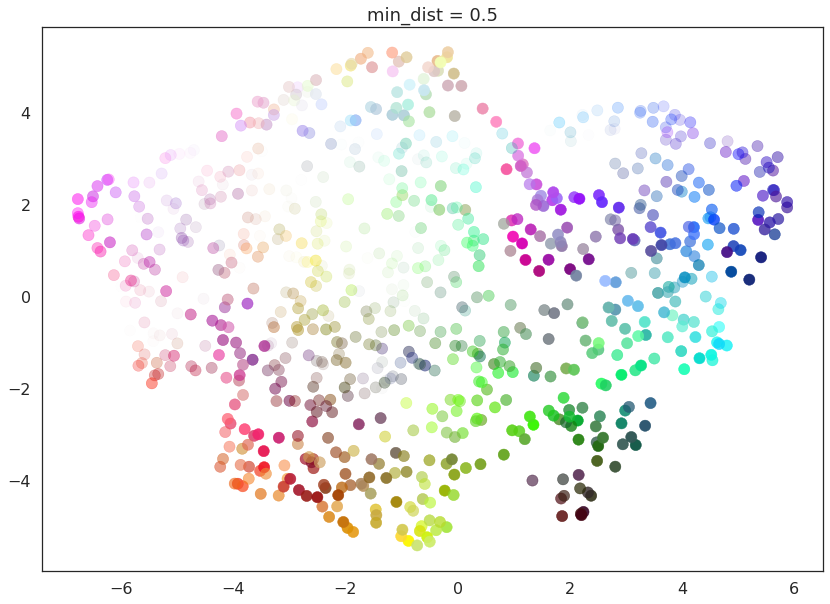
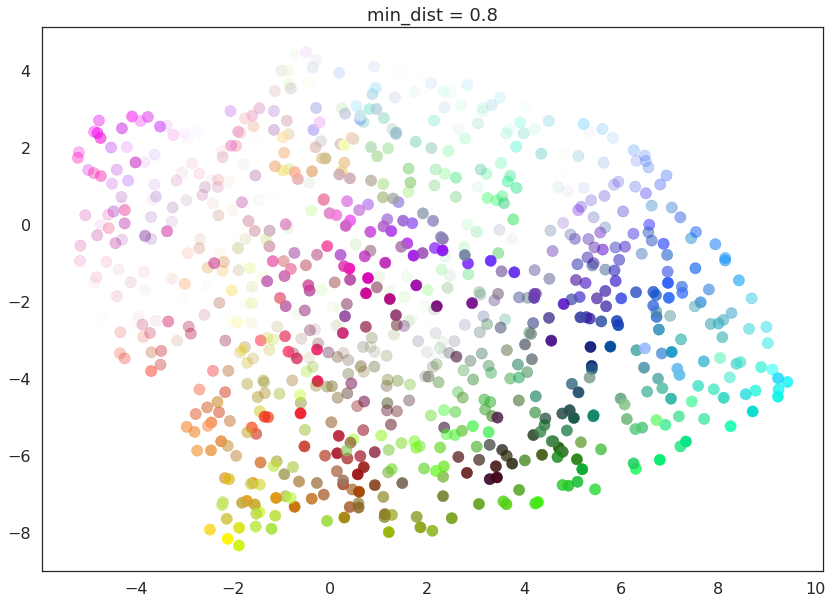
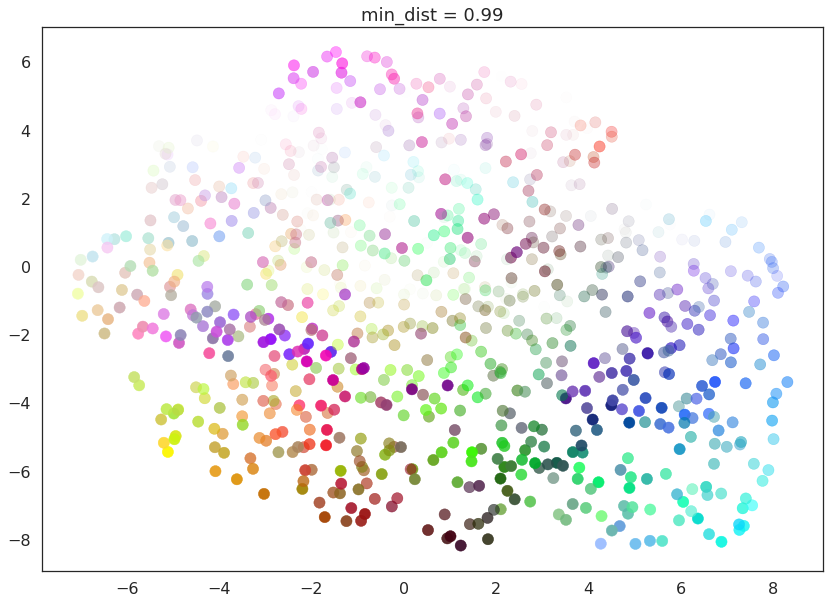
在这里我们看到,当min_dist=0.0时,UMAP 设法找到了数据中的小连接组件、簇和链,并在最终的嵌入中强调了这些特征。随着min_dist的增加,这些结构被推开,变成了更柔和、更普遍的特征,提供了数据更好的整体视图,但牺牲了更详细的拓扑结构。
n_components
作为许多scikit-learn降维算法的标准,UMAP 提供了一个n_components参数选项,允许用户确定我们将数据嵌入的降维空间的维度。与 t-SNE 等其他一些可视化算法不同,UMAP 在嵌入维度上具有良好的可伸缩性,因此您不仅可以将其用于 2 维或 3 维的可视化。
为了本次演示的目的(以便我们可以看到参数的影响),我们将只查看 1 维和 3 维嵌入,我们有一些希望能够可视化它们。
首先,我们将n_components设置为 1,强制 UMAP 将数据嵌入到一条线上。为了可视化,我们将在 y 轴上随机分布数据,以便在点之间提供一些分离。
draw_umap(n_components=1, title='n_components = 1')
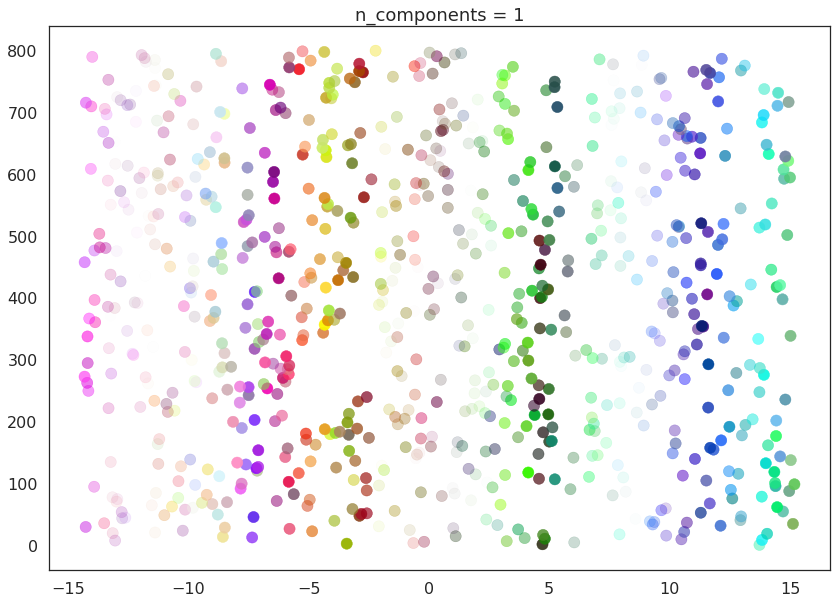
现在我们将尝试n_components=3。为了可视化,我们将利用matplotlib的基本 3 维绘图功能。
draw_umap(n_components=3, title='n_components = 3')
/opt/anaconda3/envs/umap_dev/lib/python3.6/site-packages/sklearn/metrics/pairwise.py:257: RuntimeWarning: invalid value encountered in sqrt
return distances if squared else np.sqrt(distances, out=distances)
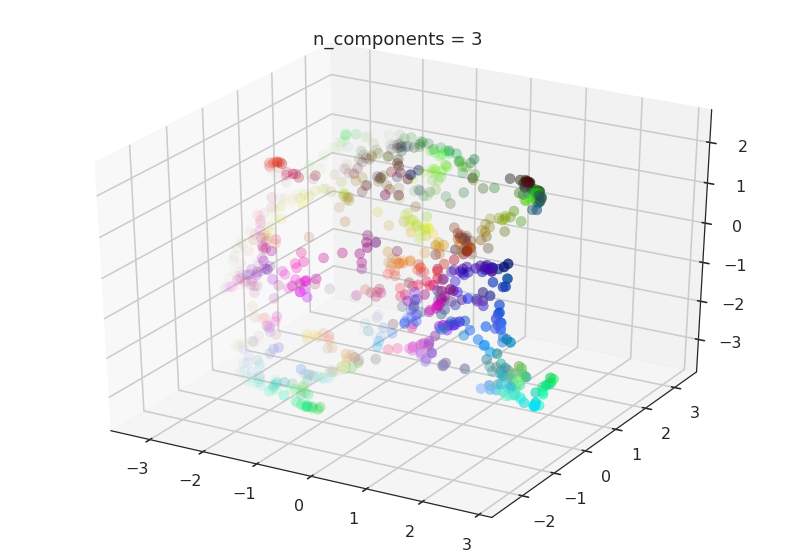
在这里我们可以看到,UMAP 在拥有更多工作维度时,可以更容易地以尊重数据拓扑结构的方式分离颜色。
如前所述,并没有要求必须停在n_components=3。如果您对(基于密度的)聚类或其他机器学习技术感兴趣,选择一个更接近数据所在底层流形维度的更大嵌入维度(例如 10 或 50)可能会更有益。
metric
我们在本 Notebook 中将考虑的最后一个 UMAP 参数是metric参数。它控制在输入数据的环境空间中如何计算距离。默认情况下,UMAP 支持多种度量,包括
闵可夫斯基类度量
euclidean
manhattan
chebyshev
minkowski
其他空间度量
canberra
braycurtis
haversine
归一化空间度量
mahalanobis
wminkowski
seuclidean
角度和相关性度量
cosine
correlation
二进制数据度量
hamming
jaccard
dice
russellrao
kulsinski
rogerstanimoto
sokalmichener
sokalsneath
yule
预计算
所有上述度量都假设您的输入数据在某个 N 维空间中是“原始”的。有时,您已经计算了点之间的成对距离,并且您的输入数据是一个距离/相似度矩阵。在这种情况下,您可以执行类似UMAP(metric='precomputed').fit_transform(<distance matrix>)的操作。
您可以通过设置metric='<metric name>'来指定任何一个;例如,要使用余弦距离作为度量,您将使用metric='cosine'。
然而,UMAP 提供的不止这些——它支持自定义的用户定义度量,只要这些度量可以通过 numba 在nopython模式下编译。在本 Notebook 中,我们将查看此类自定义度量。要定义此类度量,我们需要 numba ……
import numba
对于我们的第一个自定义度量,我们将距离定义为红色通道差值的绝对值。
@numba.njit()
def red_channel_dist(a,b):
return np.abs(a[0] - b[0])
为了更具探索性,进行一些颜色空间转换会很有用——为了简单起见,我们将只使用 HSL 公式从 (R,G,B) 元组中提取色相、饱和度和亮度。
@numba.njit()
def hue(r, g, b):
cmax = max(r, g, b)
cmin = min(r, g, b)
delta = cmax - cmin
if cmax == r:
return ((g - b) / delta) % 6
elif cmax == g:
return ((b - r) / delta) + 2
else:
return ((r - g) / delta) + 4
@numba.njit()
def lightness(r, g, b):
cmax = max(r, g, b)
cmin = min(r, g, b)
return (cmax + cmin) / 2.0
@numba.njit()
def saturation(r, g, b):
cmax = max(r, g, b)
cmin = min(r, g, b)
chroma = cmax - cmin
light = lightness(r, g, b)
if light == 1:
return 0
else:
return chroma / (1 - abs(2*light - 1))
有了这个基础,我们可以定义三个额外的距离。第一个简单地测量色相的差异,第二个测量组合饱和度和亮度空间中的欧几里得距离,而第三个测量完整 HSL 空间中的距离。
@numba.njit()
def hue_dist(a, b):
diff = (hue(a[0], a[1], a[2]) - hue(b[0], b[1], b[2])) % 6
if diff < 0:
return diff + 6
else:
return diff
@numba.njit()
def sl_dist(a, b):
a_sat = saturation(a[0], a[1], a[2])
b_sat = saturation(b[0], b[1], b[2])
a_light = lightness(a[0], a[1], a[2])
b_light = lightness(b[0], b[1], b[2])
return (a_sat - b_sat)**2 + (a_light - b_light)**2
@numba.njit()
def hsl_dist(a, b):
a_sat = saturation(a[0], a[1], a[2])
b_sat = saturation(b[0], b[1], b[2])
a_light = lightness(a[0], a[1], a[2])
b_light = lightness(b[0], b[1], b[2])
a_hue = hue(a[0], a[1], a[2])
b_hue = hue(b[0], b[1], b[2])
return (a_sat - b_sat)**2 + (a_light - b_light)**2 + (((a_hue - b_hue) % 6) / 6.0)
有了这些自定义度量,我们可以让 UMAP 使用这些度量来衡量输入数据点之间的距离,从而嵌入数据。请注意,numba在定义距离函数方面提供了显著的灵活性。尽管如此,即使使用此类自定义函数,我们也能保持 UMAP 的高性能。
for m in ("euclidean", red_channel_dist, sl_dist, hue_dist, hsl_dist):
name = m if type(m) is str else m.__name__
draw_umap(n_components=2, metric=m, title='metric = {}'.format(name))
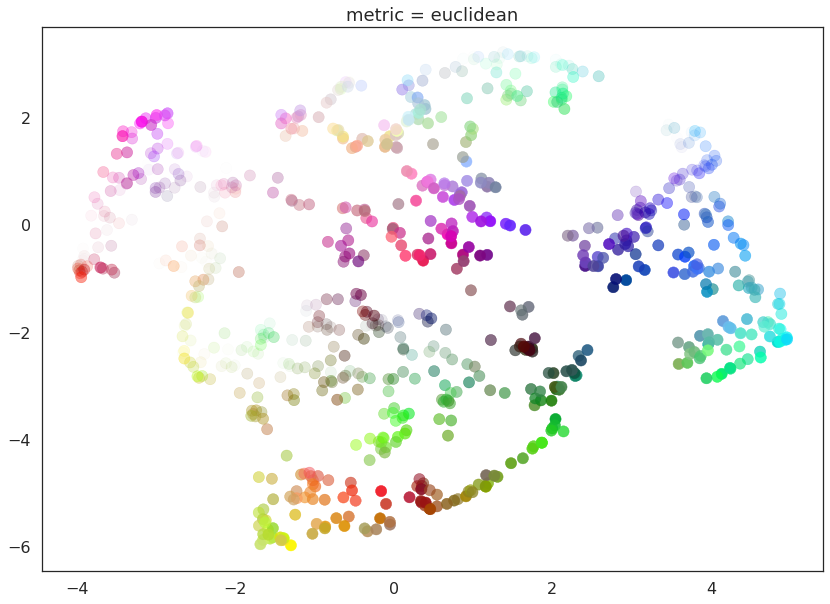
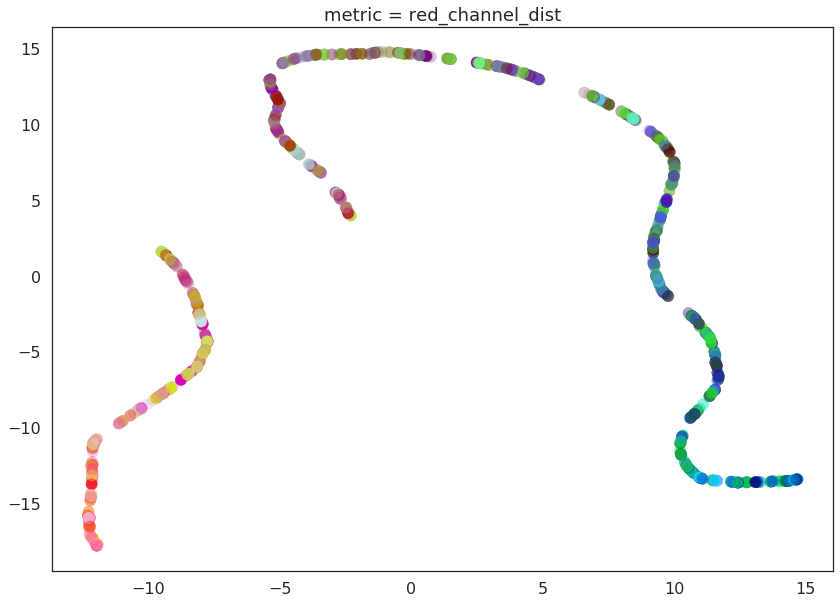
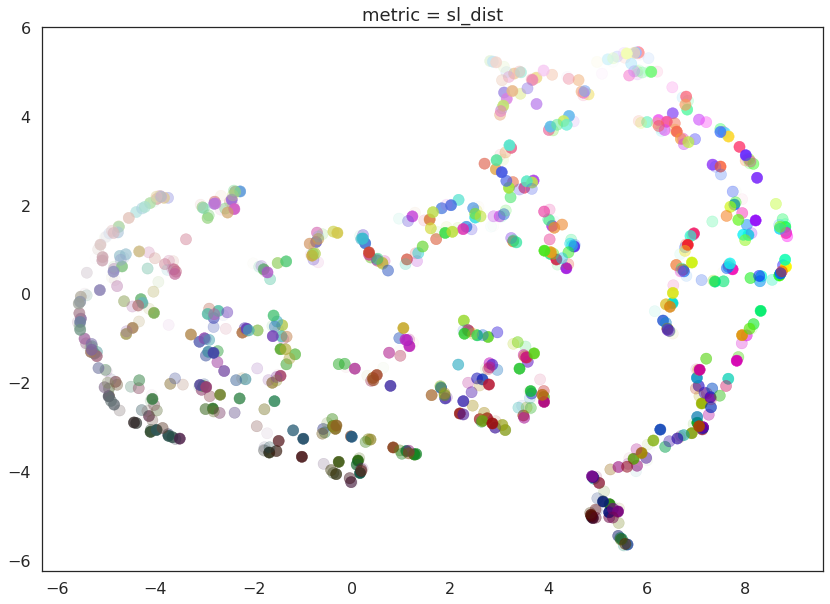
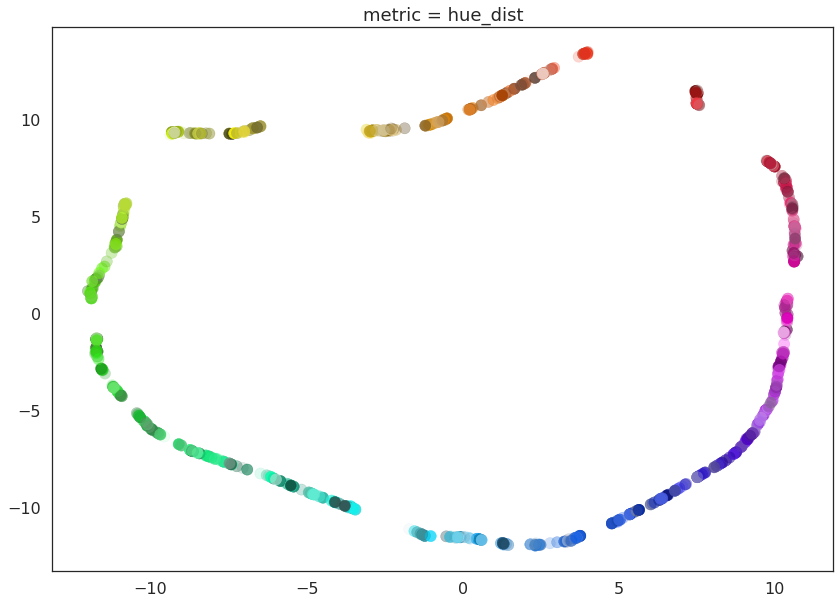
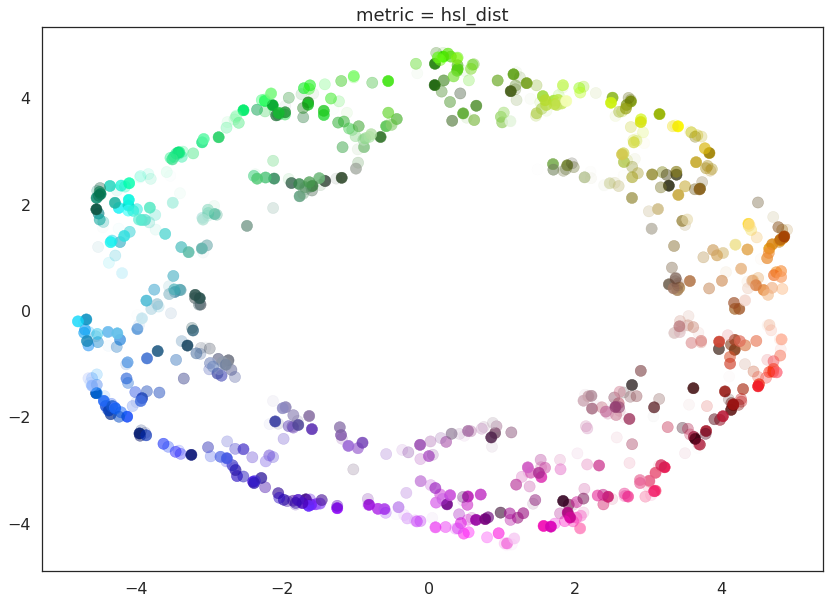
在这里我们可以清楚地看到这些度量的影响。纯红色通道正确地将数据视为存在于一维流形上,色相度量将数据解释为存在于一个圆中,而 HSL 度量根据饱和度和亮度使圆变厚。这合理地展示了 UMAP 在理解数据底层拓扑结构并找到该拓扑结构的合适低维表示方面的强大功能和灵活性。